
 如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.
如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.分析 (1)只要证明△FCG≌△EDG,可得FG=EG,结合CG=GD即可证明;
(2))①如图四边形CEDF是矩形时,在Rt△CDF中,CD=AB=3,∠DCF=60°,∠CFD=90°,易知CF=$\frac{1}{2}$CD=$\frac{3}{2}$.由ED=CF=$\frac{3}{2}$,即可推出AE=AD-DE=$\frac{7}{2}$;
②如图四边形CEDF是菱形时,易知△CDF,△CDE都是等边三角形,推出DE=CD=AB=3,可得AE=AD-ED=5-3=2;
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FCG=∠EDG,∠CFG=∠DEG,又CG=DG.
∴△FCG≌△EDG,
∴FG=EG.
∴四边形CEDF是平行四边形.
(2)①如图四边形CEDF是矩形时,在Rt△CDF中,CD=AB=3,∠DCF=60°,∠CFD=90°,
∴CF=$\frac{1}{2}$CD=$\frac{3}{2}$.
∵ED=CF=$\frac{3}{2}$,
∴AE=AD-DE=$\frac{7}{2}$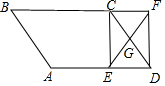
②如图四边形CEDF是菱形时,易知△CDF,△CDE都是等边三角形,
∴DE=CD=AB=3,
∴AE=AD-ED=5-3=2.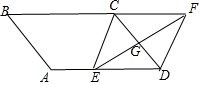
故答案为$\frac{7}{2}$,2.
点评 本题考查平行四边形的性质、矩形、菱形的性质、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 10x3y4=2xy•5x2y3 | B. | 4a2-4ab+b2=(2a-b)2 | ||
| C. | (a-b)(a+b)=a2-b2 | D. | x2+3x-5=(x-1)(x+4)-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
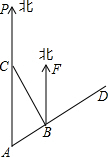 如图,我军两艘巡洋舰在南海某海域执行巡逻任务,两舰自A处沿AD方向航行,巡逻到B处后,1号舰沿原来的方向继续前行,2号舰则沿北偏西方向航行到C处(C在A的正北方向)后改变航线,计划沿与1号舰航线平行,且方向相同的路线航行.
如图,我军两艘巡洋舰在南海某海域执行巡逻任务,两舰自A处沿AD方向航行,巡逻到B处后,1号舰沿原来的方向继续前行,2号舰则沿北偏西方向航行到C处(C在A的正北方向)后改变航线,计划沿与1号舰航线平行,且方向相同的路线航行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
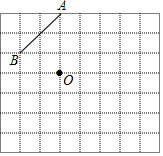 如图,在正方形网格上有A、B、O三点,如果用(3,3)表示方格纸上A点的位置,(1,1)表示B点的位置,O点也在网格点上.
如图,在正方形网格上有A、B、O三点,如果用(3,3)表示方格纸上A点的位置,(1,1)表示B点的位置,O点也在网格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com