
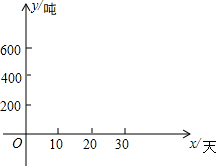
 某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.
某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.分析 (1)由题意得甲乙生产线的关系式;
(2)由(1)可知,甲乙生产线函数图象经过的点,读图求解.
解答 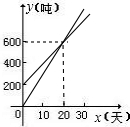 解:(1)由题意可得:甲生产线生产时对应的函数关系式是y=20x+200;
解:(1)由题意可得:甲生产线生产时对应的函数关系式是y=20x+200;
乙生产线生产时对应的函数关系式为y=30x.
(2)由(1)可知,甲生产线所对应的生产函数图象一定经过两点A(0,200)和B(20,600);
乙生产线所对应的生产函数图象一定经过两点O(0,0)和B(20,600).
因此图象如右图所示.
由图象可知:第10天结束时,甲生产线的总产量高;第30天结束时,乙生产线的总产量高
点评 此题考查一次函数的应用,关键是利用一次函数的性质解决实际问题,利用最大最小值求实际问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com