
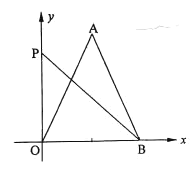
【题目】如图,已知平面直角坐标系中点![]() 坐标是
坐标是![]() ,点
,点![]() 在
在![]() 轴上,
轴上, ![]() 是
是![]() 的垂直平分线上一点,
的垂直平分线上一点,![]() 是
是![]() 轴上一点,若
轴上一点,若![]() 时,则
时,则![]() ___________.
___________.
【答案】10
【解析】
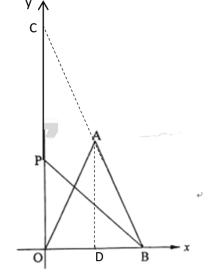
延长BA交y轴于点C,过点A作AD⊥OB于D,根据垂直平分线的性质、勾股定理、三线合一和点的坐标即可求出AO、AB、OB、AD的长,然后利用三角形外角的性质和等角对等边可得AC=AO,从而求出BC,根据勾股定理即可求出OC,再利用三角形外角的性质和等角对等边可得PB=PC,从而得出结论.
解:延长BA交y轴于点C,过点A作AD⊥OB于D
∵点![]() 坐标是
坐标是![]() ,是
,是![]() 的垂直平分线上一点
的垂直平分线上一点
∴AO=AB ,OB=2OD=4, ∠OAB =2∠OAD,AD=5
根据勾股定理可得AB= AO=![]()
∵PO⊥x轴
∴AD∥PO
∴∠OAD=∠AOP
∴∠OAB =2∠AOP
∵∠OAB=∠AOP+∠ACO
∴∠AOP=∠ACO
∴AC=AO=![]()
∴BC=AB+AC=![]()
根据勾股定理可得OC=![]()
∵![]()
∴∠OPB=2∠AOP=2∠ACO
∵∠OPB=∠ACO+∠ABP
∴∠ACO=∠ABP
∴PB=PC
∴![]() PO+PC=OC=10
PO+PC=OC=10
故答案为:10.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件,第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.

(1)图中点P所表示的实际意义是 ;销售单价每提高1元时,销售量相应减少 件;
(2)请直接写出y与x之间的函数表达式: ;自变量x的取值范围为 ;
(3)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“天生雾、雾生露、露生耳”,银耳是一种名贵食材,富含人体所需的多种氨基酸和微量元素,具有极高的药用价值和食用价值.某银耳培育基地的银耳成熟了,需要采摘和烘焙.现准备承包给甲和乙两支专业采摘队,若承包给甲队,预计12天才能完成,为了减小银耳因气候变化等原因带来的损失,现决定由甲、乙两队同时采摘,则可以提前8天完成任务.
(1)若单独由乙队采摘,需要几天才能完成?
(2)若本次一共采摘了300吨新鲜银耳,急需在9天内进行烘焙技术处理.已知甲、乙两队每日烘焙量相当,甲队单独加工(烘焙)![]() 天完成100吨后另有任务,剩下的200吨由乙队加工(烘焙),乙队刚好在规定的时间内完工.若甲、乙两队从采摘到加工,每日工资分别是600元和1000元.问:银耳培育基地此次需要支付给采摘队的总工资是多少?
天完成100吨后另有任务,剩下的200吨由乙队加工(烘焙),乙队刚好在规定的时间内完工.若甲、乙两队从采摘到加工,每日工资分别是600元和1000元.问:银耳培育基地此次需要支付给采摘队的总工资是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°,请探究图中线段BE,EF,FD之间的数量关系是什么?
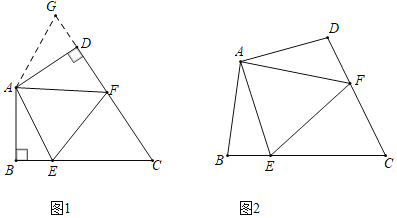
小明探究此问题的方法是:延长FD到点G,使DG=BE,连结AG.先证明△ABE≌△ADG,得AE=AG;再由条件可得∠EAF=∠GAF,证明△AEF≌△AGF,进而可得线段BE,EF,FD之间的数量关系是 .
(2)拓展应用:
如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在 ![]() 中,
中,![]() ,
,![]() 平分
平分![]() 的外角
的外角![]() ,
,![]() 与
与![]() 的垂直平分线
的垂直平分线![]() 相交于点
相交于点![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)如图②,![]() 的角平分线
的角平分线![]() 与中线
与中线![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .(直接填数值)
.(直接填数值)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com