
【题目】材料一,在平面里有两点![]() ,
,![]() ,若
,若![]() 为起点,
为起点,![]() 为终点,则把有方向且有长度的线段
为终点,则把有方向且有长度的线段![]() 叫做向量,记为:
叫做向量,记为:![]() ,并且可用坐标表示这个向量,表示方法为:
,并且可用坐标表示这个向量,表示方法为:
![]() ,向量
,向量![]() 的长度可以表示成
的长度可以表示成![]()
例如:![]() ,
,![]() 则
则![]() ,
,
即![]() 所以
所以![]()
材料二:若![]() ,
,![]() ,则
,则![]()
若![]() 时,则
时,则![]() .
.
根据材料解决下列问题:
已知![]() 中,
中,![]() ,
,![]() ,
,![]()
(1)![]() ________
________ ![]() ___________
___________
(2)当![]() 时,求证:
时,求证:![]() 是直角三角形.
是直角三角形.
(3)若![]() ,
,![]() ,求使
,求使![]() 恒成立的
恒成立的![]() 的取值范围.
的取值范围.
【答案】(1)(11,1),![]() ;(2)证明见解析;(3)m<2
;(2)证明见解析;(3)m<2
【解析】
(1)利用向量的定义和向量的长度的计算公式解答;
(2)利用两点间的距离公式和勾股定理逆定理进行证明;
(3)利用向量的乘法法则求得a、b的值;然后代入不等式,解不等式即可求得m的取值范围.
(1)∵A(3,3),B(8,4),
∴AB=(8(3),43),即AB=(11,1),
|AB|=![]()
故答案为:(11,1);![]()
(2)当x=2时,A(3,3),B(8,4),C(2,2)
此时AB2=(38)2+(43)2=122,
AC2=(32)2+[3(2)]2=50,BC2=(28)2+(24)2=72.
得AB2=AC2+BC2
∴△ABC是直角三角形.
(3)∵A(3,3),B(8,4),C(x,x)
∴AB=(11,1),AC=(x+3,x3),BC=(x8,x4)
∴a=ABAC=11x+33x3=10x+30
b=ACBC=x25x24+x2+7x+12=2x2+2x12
∴a+b=10x+30+2x2+2x12=2x2+12x+18
∴由a+b>m2得到:2x2+12x+18>m2
即:m<2x2+12x+20
∴m<2(x+3)2+2
∵2(x+3)2+22.
∴m<2
∴使a+b>m2恒成立的m的取值范围是:m<2
故答案为:m<2


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点以每秒2个单位的速度沿
点以每秒2个单位的速度沿![]() 轴向左移动.
轴向左移动.
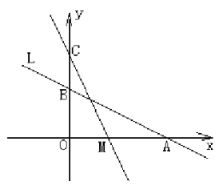
(1)求![]() 、
、![]() 两点的坐标
两点的坐标
(2)求![]() 的面积
的面积![]() 与
与![]() 的移动时间
的移动时间![]() (秒)之间的函数关系式;
(秒)之间的函数关系式;
(3)当![]() 何值时
何值时![]() ,并求此时
,并求此时![]() 点的坐标.
点的坐标.
(4)当![]() 何值时
何值时![]() 的面积是
的面积是![]() 一半,并求此时
一半,并求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
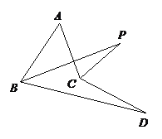
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,O为平面直角坐标系的原点,点的坐标分别为A(a,2)、B(a,-1),D(b,2).且a、b满足![]() .点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
.点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
(1)点C的坐标为_______________
(2)当点P移动在线段BC上时,求三角形ACP的面积(用含t的代数式表示)
(3)在移动过程中,当三角形ACP的面积是5时,直接写出点P移动的时间为几秒

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
A.15°B.20°C.25°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD、MN相交与点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角: .
(2)若∠AOC=![]() ∠FOM,求∠MOD与∠AON的度数.
∠FOM,求∠MOD与∠AON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可变形为
b2=0可变形为
![]() ,
,
根据a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的两个不相等的实数根,
1=0的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com