练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    一个等边三角形的边长为4，则这个等边三角形的面积为
     
    ．
    分析：作出等边三角形边上高，利用60°的正弦值可得高的值，利用三角形的面积公式求解即可．
    解答：精英家教网解：如图，作AD⊥BC于点D．
    ∴AD=AB×sin∠B=
    		3
    2
    ×4=2
    		3
    ，
    ∴边长为a的等边三角形的面积为
    1
    2
    ×4×2
    		3
    =4
    		3
    ，故答案为4
    		3
    ．
    点评：考查三角形的面积的求法；利用60°的正弦值得到等边三角形一边上的高是解决本题的突破点．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

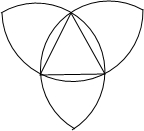    精英家教网已知一个等边三角形的边长为2，分别以它的三个顶点为圆心，边长为半径画弧，得到右图，那么图中所有的弧长的和是（　　）
    A、4πB、6πC、8πD、10π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    11、如图，一个等边三角形的边长与和它的一边相切的圆的周长相等，当此圆按箭头方向从某一位置沿等边三角形的三边作无滑动滚动，直至回到原出发位置时，则该圆转了（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    △ABC是一块等边三角形的废铁片，利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F、G分别落在AC、AB上．
    Ⅰ、证明：△BDG≌△CEF；
    Ⅱ、探究：怎样在铁片上准确地画出正方形．
    小聪和小明各给出了一种想法，请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答．如果两题都解，只以Ⅱa的解答记分．
    Ⅱa、小聪想：要画出正方形DEFG，只要能计算出正方形的边长就能求出BD和CE的长，从而确定D点和E点，再画正方形DEFG就容易了．
    设△ABC的边长为2，请你帮小聪求出正方形的边长．（结果用含根号的式子表示，不要求分母有理化）
    Ⅱb、小明想：不求正方形的边长也能画出正方形．具体作法是：
    ①在AB边上任取一点G′，如图作正方形G′D′E′F′；
    ②连接BF′并延长交AC于F；
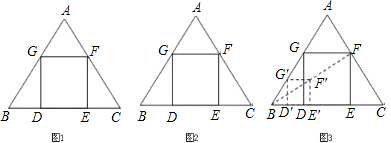    ③作FE∥F′E′交BC于E，FG∥F′G′交AB于G，GD∥G′D′交BC于D，则四精英家教网边形DEFG即为所求．
    你认为小明的作法正确吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个等边三角形的边长为
    		2
    ，则其面积为
    		3
    2
    		3
    2
    ．

    查看答案和解析>>

    同步练习册答案