
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}>0$;③ac-b+1=0;④OA•OB=-$\frac{c}{a}$.其中正确结论的序号是①③④.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}>0$;③ac-b+1=0;④OA•OB=-$\frac{c}{a}$.其中正确结论的序号是①③④. 分析 观察函数图象,根据二次函数图象与系数的关系找出“a<0,c>0,-$\frac{b}{2a}$>0”,再由顶点的纵坐标在x轴上方得出$\frac{4ac-{b}^{2}}{4a}$>0.①由a<0,c>0,-$\frac{b}{2a}$>0即可得知该结论成立;②由顶点纵坐标大于0即可得出该结论不成立;③由OA=OC,可得出xA=-c,将点A(-c,0)代入二次函数解析式即可得出该结论成立;④结合根与系数的关系即可得出该结论成立.综上即可得出结论.
解答 解:观察函数图象,发现:
开口向下⇒a<0;与y轴交点在y轴正半轴⇒c>0;对称轴在y轴右侧⇒-$\frac{b}{2a}$>0;顶点在x轴上方⇒$\frac{4ac-{b}^{2}}{4a}$>0.
①∵a<0,c>0,-$\frac{b}{2a}$>0,
∴b>0,
∴abc<0,①成立;
②∵$\frac{4ac-{b}^{2}}{4a}$>0,
∴$\frac{{b}^{2}-4ac}{4a}$<0,②不成立;
③∵OA=OC,
∴xA=-c,
将点A(-c,0)代入y=ax2+bx+c中,
得:ac2-bc+c=0,即ac-b+1=0,③成立;
④∵OA=-xA,OB=xB,xA•xB=$\frac{c}{a}$,
∴OA•OB=-$\frac{c}{a}$,④成立.
综上可知:①③④成立.
故答案为:①③④.
点评 本题考查了二次函数图象与系数的关系以及根与系数的关系,解题的关键是观察函数图象逐条验证四条结论.本题属于基础题,难度不大,解决该题型题目时,观察函数图形,利用二次函数图象与系数的关系找出各系数的正负是关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | -6 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
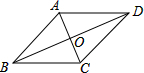 如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | OA=OC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
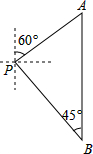 如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?
如图,小明从P点出发,沿北偏东60°方向行驶到达A处,接着向正南方向行驶100($\sqrt{3}$+1)米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com