
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
【答案】
(1)
解:∵B(4,m)在直线y=x+2上,
∴m=6,即B(4,6),
∵A( ![]() ,
, ![]() )和B(4,6)在抛物线y=ax2+bx+6上,
)和B(4,6)在抛物线y=ax2+bx+6上,
∴ 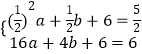 ,
,
解得: ![]() ,
,
∴抛物线的解析式y=2x2﹣8x+6
(2)
解:存在.
设动点P的坐标为(n,n+2),点C的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6)=﹣2n2+9n﹣4=﹣2(n﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣2<0,
∴开口向下,有最大值,
∴当n= ![]() 时,线段PC有最大值
时,线段PC有最大值 ![]()
【解析】(1)将点B坐标代入直线解析式,求出m的值,然后把A、B坐标代入二次函数解析式,求出a、b,即可求得解析式;(2)设动点P的坐标为(n,n+2),点C的坐标为(n,2n2﹣8n+6),表示出PC的长度,然后利用配方法求出二次函数的最大值,并求出此时n的值.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】班级准备召开主题班会,现从由3名男生和2名女生所组成的班委中,随机选取两人担任主持人,求两名主持人恰为一男一女的概率.(请用“画树状图”或“列表”等方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(﹣3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数),使平移后的图象的顶点在x轴上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)
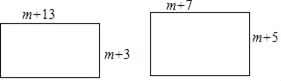
(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;
(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.
(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 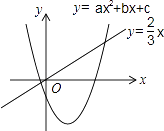
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
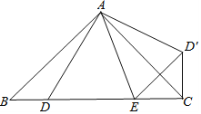
【题目】如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.
(1)当∠DAE=45°时,求证:DE=D′E;
(2)在(1)得条件下,猜想:BD2、DE2、CE2有怎样的数量关系?请写出,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣2=0
(1)若该方程的一个根为1,求m的值及该方程的另一根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com