
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
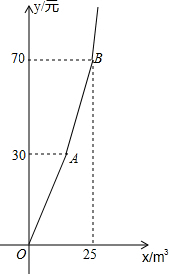 为加强公路的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为两个阶梯,一、二阶梯用水的单价之比等于1:2,如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系,其中射线AB表示第二级阶梯时y与x之间的函数关系.
为加强公路的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为两个阶梯,一、二阶梯用水的单价之比等于1:2,如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系,其中射线AB表示第二级阶梯时y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
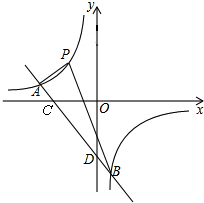 在反比例函数图象上且到x轴、y轴距离相等.
在反比例函数图象上且到x轴、y轴距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
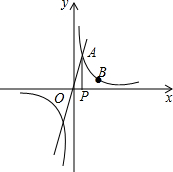 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点A,过点A作x轴的垂线,垂足为点P,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点A,过点A作x轴的垂线,垂足为点P,已知△OAP的面积为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com