
【题目】如图,直线y= ![]() x+1与y轴交于A点,过点A的抛物线y=﹣
x+1与y轴交于A点,过点A的抛物线y=﹣ ![]() x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).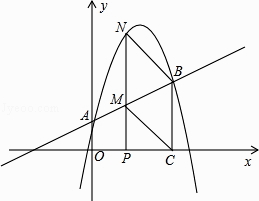
(1)直接写出抛物线的解析式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
【答案】
(1)
解:∵BC⊥x轴,垂足为点C,C(3,0),
∴B的横坐标为3.
将x=3代入y= ![]() x+1得:y=
x+1得:y= ![]() .
.
∴B(3, ![]() ).
).
将x=0代入y= ![]() x+1得:y=1.
x+1得:y=1.
∴A(0,1).
将点A和点B的坐标代入得: 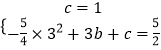 ,解得:b=
,解得:b= ![]() ,c=1.
,c=1.
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+1
x+1
(2)
解:设点P的坐标为(t,0),则N(t,﹣ ![]() t2+
t2+ ![]() t+1),M(t,
t+1),M(t, ![]() t+1).
t+1).
∴S=(﹣ ![]() t2+
t2+ ![]() t+1)﹣(
t+1)﹣( ![]() t+1)=﹣
t+1)=﹣ ![]() t2+
t2+ ![]() t.(0<t<3).
t.(0<t<3).
(3)
解:∵MN∥BC,
∴当MN=NB时,四边形BCMN为平行四边形.
∴﹣ ![]() t2+
t2+ ![]() t=
t= ![]() ,解得t=1或t=2.
,解得t=1或t=2.
∴当t=1或t=2时,四边形BCMN为平行四边形.
当t=1时,M(1, ![]() ).
).
依据两点间的距离公式可知:MC= ![]() =
= ![]() .
.
∴MN=MC.
∴四边形BCMN为菱形.
当t=2时,M(2,2),则MC= ![]() =
= ![]() .
.
∴MC≠MN.
∴此时四边形BCMN不是菱形.
综上所述,当t=1时,四边形BCMN为菱形
【解析】(1)先求得点B和点A的坐标,然后将原点坐标,点A和点B的坐标代入抛物线的解析式求解即可;(2)设点P的坐标为(t,0),则N(t,﹣ ![]() t2+
t2+ ![]() t+1),M(t,
t+1),M(t, ![]() t+1),然后依据MN等于M、N两点的纵坐标之差可得到S与t的函数关系式;(3)已知MN∥BC,故此当MN=NB时,四边形BCMN为平行四边形,然后列出方程组求解即可;当MC=MN时,四边形BCMN为菱形,然后分别将t=1和t=2代入求得点M的坐标,然后再求得MC的长,最后依据MC于是等于MN进行判断即可.
t+1),然后依据MN等于M、N两点的纵坐标之差可得到S与t的函数关系式;(3)已知MN∥BC,故此当MN=NB时,四边形BCMN为平行四边形,然后列出方程组求解即可;当MC=MN时,四边形BCMN为菱形,然后分别将t=1和t=2代入求得点M的坐标,然后再求得MC的长,最后依据MC于是等于MN进行判断即可.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 点P从A点出发沿
点P从A点出发沿![]() 路径向终点运动,终点为B点;点Q从B点出发沿
路径向终点运动,终点为B点;点Q从B点出发沿![]() 路径向终点运动,终点为A点
路径向终点运动,终点为A点![]() 点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作
点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作![]() 于E,
于E,![]() 于
于![]() 问:点P运动多少时间时,
问:点P运动多少时间时,![]() 与QFC全等?请说明理由.
与QFC全等?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题12分)小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?
答:我抽取的2张卡片是 、 ,乘积的最大值为 .
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
答:我抽取的2张卡片是 、 ,商的最小值为 .
(3)从中取出4张卡片,用学过的运算方法,使结果为24.如何抽取?写出运算式子.(写出一种即可)
答:我抽取的4张卡片是 、 、 、 ,
算24的式子为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣ ![]() ;⑤2a<b+
;⑤2a<b+ ![]() ,正确的是( )
,正确的是( )
A.①③
B.①②③
C.①②③⑤
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB:y=![]() x+
x+![]() 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )

A. (0,4) B. (0,5) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com