
【题目】如图,已知矩形ABCD中,AB=8,AD=6, 点E是边CD上一个动点,连接AE,将△AED沿直线AE翻折得△AEF.
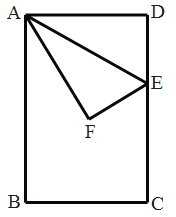
(1) 当点C落在射线AF上时,求DE的长;
(2)以F为圆心,FB长为半径作圆F,当AD与圆F相切时,求cos∠FAB的值;
(3)若P为AB边上一点,当边CD上有且仅有一点Q满∠BQP=45°,直接写出线段BP长的取值范围.
【答案】(1)DE=3;(2)![]() ;(3)BP=12
;(3)BP=12![]() -12或6<BP≤
-12或6<BP≤![]()
【解析】
(1)当点C落在射线AF上时,设DE=x,则EF=DE=x,CE=8-x,根据勾股定理,列出方程,即可求解;
(2)以F为圆心,FB长为半径作圆F,当AD与圆F相切时,设切点为M,连接FM,则FM⊥AD,过点F作FN⊥AB,设FM=x,则AN=FM=x,BF=FM=x,BN=8-x,根据勾股定理,列出方程,即可求解;
(3)以PB为底边作等腰直角三角形PMB,以点M为圆心,MP为半径作圆M,分三类:①当圆M与CD相切时,求出BP的值;②当圆M过点C时,求出BP的值;③当圆M过点D时,求出BP的值,进而,可求出BP的范围.
(1)当点C落在射线AF上时,如图1,
∵在矩形ABCD中,AB=8,AD=6,△AED沿直线AE翻折得△AEF,
∴AF=AD=6,AC=![]() ,
,
∴CF=AC-AF=10-6=4,
设DE=x,则EF=DE=x,CE=8-x,
∵在RtCFE中,![]() ,
,
∴![]() ,解得:x=3,
,解得:x=3,
∴DE=3;
(2)以F为圆心,FB长为半径作圆F,当AD与圆F相切时,如图2,
设切点为M,连接FM,则FM⊥AD,过点F作FN⊥AB,
设FM=x,则AN=FM=x,BF=FM=x,BN=8-x,
∵![]() ,
,
∴![]() ,解得:x=
,解得:x=![]() ,
,
∴cos∠FAB=![]() =
=![]() ;
;
(3)以PB为底边作等腰直角三角形PMB,以点M为圆心,MP为半径作圆M,
①当圆M与CD相切时,如图3,切点为Q,此时,边CD上有且仅有一点Q满足∠BQP=45°,
连接QM,延长QM交PB于点H,则HQ⊥CD,HQ⊥PB,
∵PMB是等腰直角三角形,
∴设PH=BH=MH=x,则PM=QM=![]() ,
,
∵HQ=AD=6,
∴x+![]() =6,解得:x=
=6,解得:x=![]() ,
,
∴BP=2x=![]()
②当圆M过点C时,如图4,此时,边CD上有两个点Q满足∠BQP=45°,
∵∠MPB=45°,∠PBC=90°,
∴BP=BC=6,
③当圆M过点D时,如图5,此时,边CD上有且仅有一点Q满足∠BQP=45°,
连接MD,过点M作MN⊥AD,MH⊥BP,
设PH=HM=HB=x,则MP=MD=![]() ,MN=AH=8-x,ND=6-x,
,MN=AH=8-x,ND=6-x,
∵在RtMND中,![]() ,
,
∴![]() ,解得:x=
,解得:x=![]() ,
,
∴BP=2×![]() =
=![]() ,
,
综上所述:线段BP长的取值范围是:BP=12![]() -12或6<BP≤
-12或6<BP≤![]() .
.

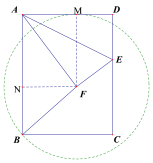
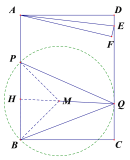
图1 图2 图3
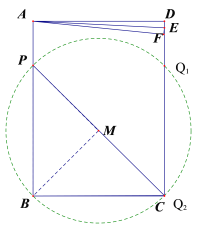
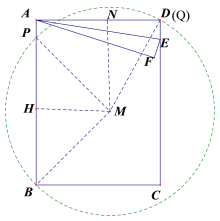
图4 图5


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】据报道,从2018年8月以来“非洲猪瘟”给生猪养殖户带来了不可估量的损失,某养殖户为了预防“非洲猪瘟”的侵袭,每天对猪场进行药熏消毒,已知一瓶药物释放过程中,一个圈舍内每立方米空气中含药量y(毫克)与时间x(分钟)之间满足正比例函数关系;药物释放完后,y与x之间满足反比例函数关系,如图所示,结合图中提供的信息解答下列问题.
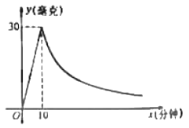
(1)分别求当![]() 和
和![]() 时,y与x之间满足的函数关系式;
时,y与x之间满足的函数关系式;
(2)据测定,当空气中每立方米的含药量不低于6毫克时,消毒才有效,那么这次熏药的有效消毒时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,如此进行下去,直至得到C10,若点P(28,m)在第10段抛物线C10上,则m的值为( )

A. 1 B. ﹣1 C. 2 D. ﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 上,连接
上,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)如图1,连接![]() ,当
,当![]() 时,求证:
时,求证:![]()
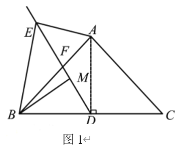
(2)如图2,当![]() 时,则线段
时,则线段![]() 之间的数量关系为 ;
之间的数量关系为 ;

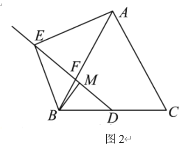
(3)在(2)的条件下,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求证:
,求证:![]() ,并求
,并求![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系x O y中,△ABC 三个顶点坐标分别为A (1, 2),B(7,2),C(5,6).
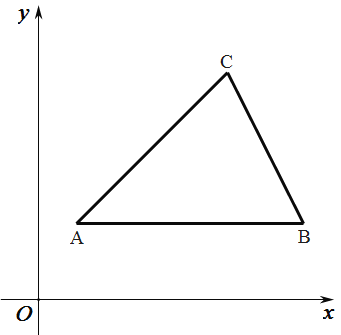
(1)在图中画出△ABC外接圆的圆心P;
(2)圆心P的坐标是______;
(3) tan∠ACB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关注数学文化:古希腊的几何学家海伦在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中,给出了如下公式:若一个三角形的三边长分别为a,b,c,记p=![]() ,则三角形的面积S=
,则三角形的面积S=![]() (海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式:
(海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式: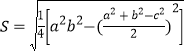 .海伦公式和秦九韶公式实质上是同一个公式,所以我们一般也称此公式为海伦-秦九韶公式.
.海伦公式和秦九韶公式实质上是同一个公式,所以我们一般也称此公式为海伦-秦九韶公式.
若△ABC的三边长分别为5,6,7,△DEF的三边长分别为![]() ,
,![]() ,
,![]() ,请选择合适的公式分别求出△ABC和△DEF的面积.
,请选择合适的公式分别求出△ABC和△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点![]() 、
、![]() ,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程
,以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程![]() 与时间
与时间![]() 满足关系
满足关系![]() ,乙以
,乙以![]() 的速度匀速运动,半圆的长度为
的速度匀速运动,半圆的长度为![]() .
.
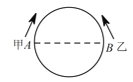
(1)甲运动![]() 后的路程是多少?
后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
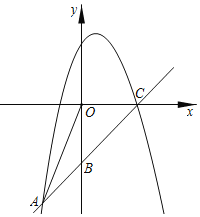
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣1,﹣5),B(0,﹣4)两点且与x轴交于点C,二次函数y=ax2+bx+4的图象经过点A、点C.
(1)求一次函数和二次函数的函数表达式;
(2)连接OA,求∠OAB的正弦值;
(3)若点D在x轴的正半轴上,是否存在以点D,C,B构成的三角形与△OAB相似?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房的成交均价由2019年8月份的8000元/![]() 下降到2019年10月份的7500元/
下降到2019年10月份的7500元/![]() .
.
(1)求2019年9、10两月该市的商品房成交均价平均每月降价的百分率(精确到0.1,参考数据:![]() );
);
(2)如果房价继续回落,按(1)的降价的百分率,你认为到2019年12月份该市的商品房成交均价会跌破7000元/![]() 吗?请说明理由.
吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com