
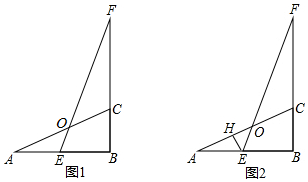
分析 (1)作辅助线,根据全等得:CD=AE=t,利用平行线分线段成比例定理列式可求得t的值;
(2)如图2,同理作辅助线,得CD=$\frac{t(4-t)}{t+1}$,利用勾股定理求AC=2$\sqrt{5}$,根据同角的三角函数列式:cos∠A=$\frac{AH}{AE}=\frac{AB}{AC}$,得AH=$\frac{2\sqrt{5}}{5}$t,证明△DOC∽△EOA,求OA=$\frac{2\sqrt{5}(t+1)}{5}$,从而得:OH=OA-AH=$\frac{2\sqrt{5}}{5}$;
(3)如图3,先画图形确定P点的路径长PP′,根据勾股定理求出即可.
解答 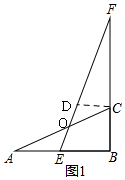 解:(1)如图1,过C作CD∥AB,交EF于D,
解:(1)如图1,过C作CD∥AB,交EF于D,
∴∠CDO=∠AEO,
∵AO=OC,∠AOE=∠DOC,
∴△AOE≌△COD,
∴AE=CD,
由题意得:AE=t,FC=2t,
∴EB=4-t,FB=2t+2,
∵CD∥EB,
∴$\frac{CD}{EB}=\frac{FC}{FB}$,
∴$\frac{t}{4-t}=\frac{2t}{2+2t}$,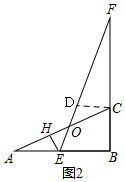
t=$\frac{3}{2}$;
(2)如图2,过C作CD∥AB,交EF于D,
∴$\frac{CD}{BE}=\frac{FC}{FB}$,
∴$\frac{CD}{4-t}=\frac{2t}{2t+2}$,
∴CD=$\frac{t(4-t)}{t+1}$,
由勾股定理得:AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
在Rt△AEH和Rt△ACB中,cos∠A=$\frac{AH}{AE}=\frac{AB}{AC}$,
∴$\frac{AH}{t}=\frac{4}{2\sqrt{5}}$,
∴AH=$\frac{2\sqrt{5}}{5}$t,
∵CD∥AB,
∴△DOC∽△EOA,
∴$\frac{DC}{AE}=\frac{OC}{OA}$,
∴$\frac{\frac{t(4-t)}{t+1}}{t}=\frac{AC-OA}{OA}$,
∴OA=$\frac{2\sqrt{5}(t+1)}{5}$,
∴OH=OA-AH=$\frac{2\sqrt{5}}{5}$;
(3)如图3,当E在A处,F在C处时,EF中点为AC中点P′,
当E在B处时,F在BC的延长线上,此时EF中点为P,
∴FC=2AB=8,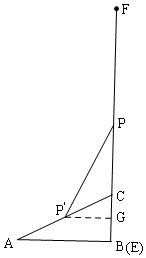
∴BF=BC+FC=2+8=10,
∴PF=$\frac{1}{2}$BF=5,
∴PC=FC-PF=8-5=3,
过P′作P′G∥AB,交BC于G,
∴P′G=$\frac{1}{2}$AB=2,
∴PG=PC+CG=3+1=4,
由勾股定理得:PP′=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
则当E点从A运动到B点,P点的路径长为2$\sqrt{5}$,
故答案为:2$\sqrt{5}$.
点评 本题是三角形的综合题,考查了全等三角形的性质和判定、相似三角形的性质和判定、动点运动问题,此类问题确定动点的路程是关键,并利用数形结合的思想综合解决问题,属于常考题型.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
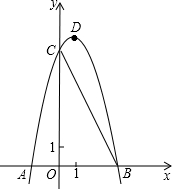 如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(-2,0),B两点,与y轴交于C点,tan∠ABC=2.
如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(-2,0),B两点,与y轴交于C点,tan∠ABC=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(4) | C. | (1)(2)(4) | D. | (2)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
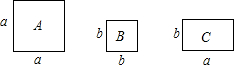 如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个边长为(a+2b)的大正方形,则需要B类卡片( )张.
如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个边长为(a+2b)的大正方形,则需要B类卡片( )张.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,-2),请你帮她画出坐标系,并写出其他各景点的坐标.
王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,-2),请你帮她画出坐标系,并写出其他各景点的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com