
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列四个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:∵抛物线开口向下,交y轴于正半轴,
∴a<0,c>0,
∴ac<0,故①正确;
∵x=1时,y<0,
∴a+b+c<0,故②错误;
由图象可知:当x=-2时,y<0,
∴4a-2b+c<0,故③正确;
由抛物线交x轴于两点,
∴b2-4ac>0,
∴4ac-b2<0,故④错误;
故选B.
点评 本题考查图象与二次函数系数之间的关系,二次函数与方程之间的转换,根的判别式的熟练运用.会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=a-b+c,然后根据图象判断其值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
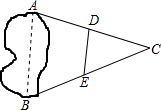 如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.
如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下:
超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
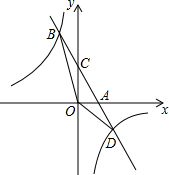 如图,在平面直角坐标系中,直线AB与x轴交于点A(1,0),与反比例函数在第二象限内的图象交于B(-1,n),连接BO,若S△AOB=2.
如图,在平面直角坐标系中,直线AB与x轴交于点A(1,0),与反比例函数在第二象限内的图象交于B(-1,n),连接BO,若S△AOB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com