
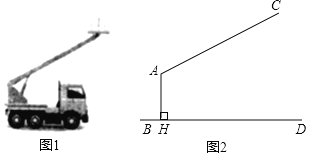
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
【答案】操作平台C离地面的高度为7.6m.
【解析】作CE⊥BD于F,AF⊥CE于F,如图2,易得四边形AHEF为矩形,则EF=AH=3.4m,∠HAF=90°,再计算出∠CAF=28°,则在Rt△ACF中利用正弦可计算出CF,然后计算CF+EF即可.
作CE⊥BD于F,AF⊥CE于F,如图2,
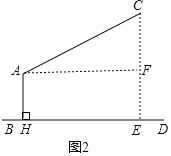
易得四边形AHEF为矩形,
∴EF=AH=3.4m,∠HAF=90°,
∴∠CAF=∠CAH-∠HAF=118°-90°=28°,
在Rt△ACF中,∵sin∠CAF=![]() ,
,
∴CF=9sin28°=9×0.47=4.23,
∴CE=CF+EF=4.23+3.4≈7.6(m),
答:操作平台C离地面的高度为7.6m.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
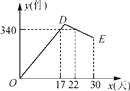
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个工人师傅要将一个正方形ABCD的余料,修剪成四边形ABEF的零件,其中CE=![]() BC,F是CD的中点.
BC,F是CD的中点.
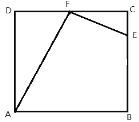
(1)若正方形的边长为a,试用含a的代数式表示AF2+EF2的值;
(2)连结AE,△AEF是直角三角形吗?为什么?(正方形的四条边都相等,四个角都是直角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,已知某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解答下列问题.
(1)分别写出当0≤x≤100和x>100时,y与x间的函数关系式;
(2)若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元,则该用户该月用了多少度电?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.
(1)如图1,求证:∠CAE=∠CBD;
(2)如图2,F是BD的中点,求证:AE⊥CF;
(3)如图3,F,G分别是BD,AE的中点,若AC=2![]() ,CE=1,求△CGF的面积.
,CE=1,求△CGF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
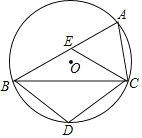
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
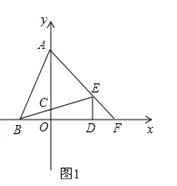
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
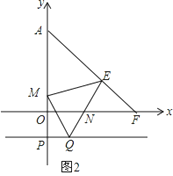
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
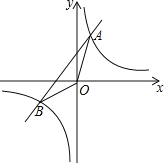
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com