
| 10 |
| 10 |
| x2+1 |
| (4-x)2+4 |
| x2+1 |
| (4-x)2+4 |
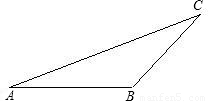
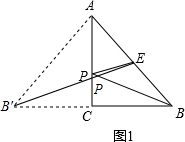 解:(1)如图1所示,作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小.连接AB′.
解:(1)如图1所示,作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小.连接AB′.| AC2+BC2 |
| 22+22 |
| 2 |
| 1 |
| 2 |
| 2 |
| B′A2+AE2 |
(2
|
| 10 |
| 10 |
| 3 |
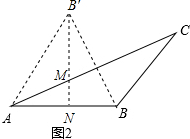
 (3)构造图形如图3所示,
(3)构造图形如图3所示,| x2+1 |
| (4-x)2+4 |
| C′E2+DE2 |
| 42+32 |


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
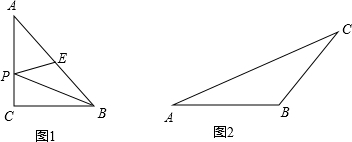
 某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:
某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:| x2+1 |
| (4-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:
某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题: (0≤x≤4)的最小值.
(0≤x≤4)的最小值.查看答案和解析>>
科目:初中数学 来源:2010年安徽省阜阳市十一中中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com