
【题目】综合与探究
如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,抛物线的对称轴交抛物线于点
,抛物线的对称轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
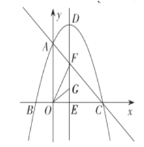
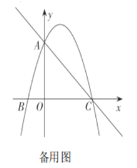
(1)求抛物线的函数表达式及其对称轴:
(2)点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上任意一点,点
是抛物线上任意一点,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是平面上任意一点,是否存在这样的点
是平面上任意一点,是否存在这样的点![]() ,
,![]() ,
,![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形,若存在,请直接写出点
为顶点的四边形是正方形,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;x=2;(2)
;x=2;(2)![]() ;(3)Q点的坐标为
;(3)Q点的坐标为![]() .
.
【解析】
(1)将点B、C坐标代入即可得出抛物线解析式,再根据求对称轴公式![]() 求对称轴即可;
求对称轴即可;
(2)先根据直线解析式以及抛物线解析式求出点F的坐标,得出![]() ,再根据
,再根据![]() 可得出
可得出![]() ,从而确定点G的坐标;
,从而确定点G的坐标;
(3)通过分析当CP为正方形的边且M位于直线下方抛物线上时可得出以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形,画出示意图,再根据正方形的性质求解即可.
为顶点的四边形是正方形,画出示意图,再根据正方形的性质求解即可.
解:(1)∵抛物线![]() 经过
经过![]() ,
,![]() ,
,
∴![]() 解得
解得
∴抛物线的函数表达式为![]() .
.
∴抛物线的对称轴为直线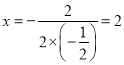 .
.
(2)∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴当![]() 时,
时,![]() .
.
∴![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]() .
.
把![]() ,
,![]() 代入
代入![]() ,得
,得![]() 解得
解得![]()
∴直线![]() 的函数表达式为
的函数表达式为![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
∴![]() .
.
(3)存在,![]() ,理由如下:
,理由如下:
若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形,则相邻的两边垂直且相等.
为顶点的四边形是正方形,则相邻的两边垂直且相等.
当CP为对角线时,则需![]() ,不存在符合条件的Q点;
,不存在符合条件的Q点;
当CP为对角线,CM为边时,若点M位于直线AC上方抛物线上时,同理需要![]() ,不存在符合条件的Q点;
,不存在符合条件的Q点;
点M位于直线AC下方抛物线上时,即点B与点M重合时,存在点Q,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形.
为顶点的四边形是正方形.
过点B作![]() ,
,

∵![]()
∴![]()
∴![]()
∵以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形
为顶点的四边形是正方形
∴![]() ,
,![]() 关于BC对称
关于BC对称
过点D作![]()
∴![]()
∵直线AC的解析式为![]()
∴当![]() 时,
时,![]()
∴![]()
∴![]()


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上点
轴上点![]() 右侧一点,以
右侧一点,以![]() ,
,![]() 为两边的菱形
为两边的菱形![]() 的顶点
的顶点![]() 落在反比例函数
落在反比例函数![]() 的图象上.
的图象上.
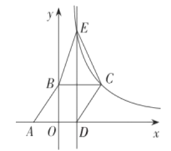
(1)求反比例函数的表达式;
(2)过点![]() 作
作![]() 轴的垂线,交反比例函数的图象于点
轴的垂线,交反比例函数的图象于点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的面积:
的面积:
(3)当![]() 时,请直接写出
时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
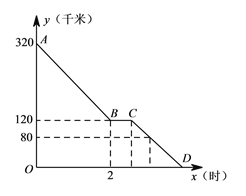
【题目】上周六上午![]() 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离![]() (千米)与他们路途所用的时间
(千米)与他们路途所用的时间![]() (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)求直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶![]() 分钟时,距姥姥家还有
分钟时,距姥姥家还有![]() 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月5日,中国邮政发行《马克思诞辰200周年》纪念邮票1套2枚(如图),这套邮票正面图案为:马克思像、马克思与恩格斯像,背面完全相同.发行当日,小宇购买了此款纪念邮票2套,他将2套邮票沿中间虚线撕开(使4枚形状、大小完全相同)后将4枚纪念邮票背面朝上放在桌面上,并随机从中抽出2张,则抽出的2张邮票恰好都是“马克思像”的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com