
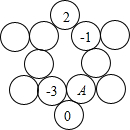
 如图所示,每一条直线上的4个圆圈都与某个二次方程x2+px+q=0及其根x1,x2相联系,中间两个数字是x1与x2,两端的两个数字为p,q,那么任一满足条件的圆圈A中的数字是0.
如图所示,每一条直线上的4个圆圈都与某个二次方程x2+px+q=0及其根x1,x2相联系,中间两个数字是x1与x2,两端的两个数字为p,q,那么任一满足条件的圆圈A中的数字是0. 分析 以2为系数、-1为根的方程x2+px+q=0有如下两种情况:①若p=2,x1=-1,即x2+2x+q=0;求出q的值及方程的另一个根,继而可设以1为系数、-3和A为根的方程为x2+p1x+q1=0,以0为系数、-1和A为根的方程为x2+p2x+q2=0,由韦达定理可得$\left\{\begin{array}{l}{-3+A=-{p}_{1}}&{①}\\{-3A={q}_{1}}&{②}\\{-1+A=-{p}_{2}}&{③}\\{-A={q}_{2}}&{④}\end{array}\right.$,就此时所有可能p1=1,p2=0、p1=1,q2=0、q1=1,p2=0、q1=1,q2=0分别求出A的值,从而得出判断;②若q=2,x2=-1,即x2+px+2=0;与①同理可得.
解答 解:以2为系数、-1为根的方程x2+px+q=0有如下两种情况:
1、若p=2,x1=-1,即x2+2x+q=0,
将x1=-1代入x2+2x+q=0,得:q=1,
即方程为x2+2x+1=0,
解得:x1=x2=-1,
如图1:
设以1为系数、-3和A为根的方程为x2+p1x+q1=0,以0为系数、-1和A为根的方程为x2+p2x+q2=0,
则$\left\{\begin{array}{l}{-3+A=-{p}_{1}}&{①}\\{-3A={q}_{1}}&{②}\\{-1+A=-{p}_{2}}&{③}\\{-A={q}_{2}}&{④}\end{array}\right.$,
若p1=1,p2=0,代入①得:A=2,代入③得A=1,不符合题意;
若p1=1,q2=0,代入①得A=2,代入④得A=0,不符合题意;
若q1=1,p2=0,代入②得A=-$\frac{1}{3}$,代入③得A=1,不符合题意;
若q1=1,q2=0,代入②得A=-$\frac{1}{3}$,代入④得A=0,不符合题意;
2、若q=2,x2=-1,即x2+px+2=0,
将x2=-1代入x2+px+2=0,得:p=3,
即方程为x2+3x+2=0,
解得:x1=-2,x2=-1,
如图2,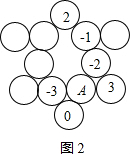
设以3为系数、-3和A为根的方程为x2+p1x+q1=0,以0为系数、-2和A为根的方程为x2+p2x+q2=0,
则$\left\{\begin{array}{l}{-3+A=-{p}_{1}}&{①}\\{-3A={q}_{1}}&{②}\\{-2+A=-{p}_{2}}&{③}\\{-2A={q}_{2}}&{④}\end{array}\right.$,
若p1=3,p2=0,代入①得A=0,代入③得A=2,不符合题意;
若p1=3,q2=0,代入①得A=0,代入④得A=0,符合题意;
若q1=3,p2=0,代入②得A=-1,代入③得A=2,不符合题意;
若q1=3,q2=0,代入②得A=-1,代入④得A=0,不符合题意;
综上,任一满足条件的圆圈A中的数字是0,
故答案为:0.
点评 本题主要考查方程的解和解方程的能力及根与系数的关系,解题的关键是根据图中数字的分布罗列所有的可能结果.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
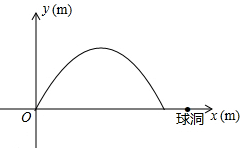 如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{16}{5}$x,其中y(m)是球的飞行速度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有4m.
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{16}{5}$x,其中y(m)是球的飞行速度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有4m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y=-(x+2)2+1 | … | … | 0 | 1 | 0 | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com