

���� ��1�����������ε����ʿɵ�DA=AB��Ȼ��֤����BAF=��ADE�������ɡ�ADE�͡�ABFȫ�ȣ�����ȫ�������ε����ʿɵ�BF=AE��AF=DE���ٸ����߶εĺͲ��ϵ�Լ����������ɵ�AF-BF=EF��
��2������֤����ADE�͡�ABFȫ�ȣ�����ȫ�������ε����ʿɵ�BF=AE��Ȼ��ɵ�BF-AF=EF��
��3������ͬ��1������˵����ADE�͡�ABFȫ�ȣ��ó�DE=AF��BF=AE��ֻ��������Ľ�����EF=AF+BF��
��� 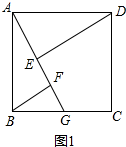 �⣺��1����ͼ1��AF-BF=EF��
�⣺��1����ͼ1��AF-BF=EF��
���ı���ABCD�������Σ�BF��AG��DE��AG��
��DA=AB����BAF+��DAE=��DAE+��ADE=90�㣬
���BAF=��ADE��
�ڡ�ABF�͡�DAE�У�
$\left\{\begin{array}{l}{��BAF=��ADE}\\{��AFB=��AED}\\{AB=AD}\end{array}\right.$��
���ABF�ա�DAE��AAS����
��BF=AE��AF=DE��
��AF-BF=EF��
��2����ͼ2��BF-AF=EF��
���ı���ABCD�������Σ�
���BAD=90�㣬AD=AB��
���BAF+��DAF=90�㣬
��BF��AG��
���BAF+��ABF=90�㣬
���DAF=��ABF��
��DE��AG��E��BF��AG��F��
���AFB=��AED=90�㣬
�ڡ�ADE�͡�ABF��$\left\{\begin{array}{l}{��AED=��BFA}\\{��DAF=��ABF}\\{AB=AD}\end{array}\right.$��
���ADE�ա�ABF��AAS����
��AE=BF��
��AE-AF=EF��
��BF-AF=EF��
��3���⣺��ͼ3��EF=AF+BF��
���ı���ABCD�������Σ�BF��AG��DE��AG��
��DA=AB����BAF+��DAE=��DAE+��ADE=90�㣬
���BAF=��ADE��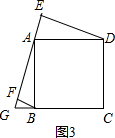
�ڡ�ABF�͡�DAE�У�
$\left\{\begin{array}{l}{��BAF=��ADE}\\{��AFB=��DEA}\\{AB=AD}\end{array}\right.$��
���ABF�ա�DAE��AAS����
��BF=AE��
��EF=AF+BF��
���� ������Ҫ�������ı����ۺ��⣬�����ε����ʺʹ�ֱ�����壬ȫ�������ε����ʺ��ж��������Ĺؼ�����������ȫ�������ε��ж������ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬��B=60�㣬BC=2����O��AC���е㣬����O��ֱ��l��AB���ཻ�ڵ�D������C��CE��AB��ֱ��l�ڵ�E�����AOD=��������������⣺
��ͼ����Rt��ABC�У���ACB=90�㣬��B=60�㣬BC=2����O��AC���е㣬����O��ֱ��l��AB���ཻ�ڵ�D������C��CE��AB��ֱ��l�ڵ�E�����AOD=��������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=$\frac{k}{8}$��x+2����x-4����kΪ��������k��0����x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��y=-$\frac{\sqrt{3}}{3}$x+b�������ߵ���һ����ΪD��
��ͼ����֪������y=$\frac{k}{8}$��x+2����x-4����kΪ��������k��0����x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��y=-$\frac{\sqrt{3}}{3}$x+b�������ߵ���һ����ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����̨�˽�ij���ӽ�Ŀ�������� | |
| B�� | �˽�ij����ѧ�������Ķ������ | |
| C�� | �˽�ij�а����������˵Ľ���״�� | |
| D�� | ���ij��ҩƷ�ڳ����¿������������ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com