
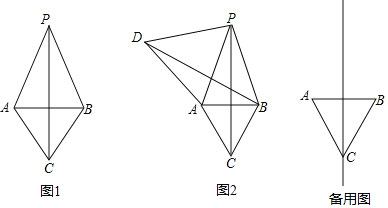
【题目】如图,△ABC是等边三角形,平面上的动点P满足PC⊥AB,记∠APB=α.
(1)如图1,当点P在直线BC上方时,直接写出∠PAC的大小(用含α的代数式表示);
(2)过点B作BC的垂线BD,同时作∠PAD=60°,射线AD与直线BD交于点D.
①如图2,判断△ADP的形状,并给出证明;
②连结CD,若在点P的运动过程中,CD=![]() AB.直接写出此时α的值.
AB.直接写出此时α的值.
【答案】(1)150°﹣![]() ;(2)①△ADP是等边三角形,证明见解析;②α=150°或α=30°.
;(2)①△ADP是等边三角形,证明见解析;②α=150°或α=30°.
【解析】
(1)由等边三角形的性质可得∠CAB=∠CBA=60°,AC=CB=AB,可证PA=PB,由等腰三角形的性质可得∠PAB=∠PBA=90°![]() ,即可求解;
,即可求解;
(2)①由“SAS”可证△DAB≌△PAC,可得AD=AP,由等边三角形的判定△ADP是等边三角形;
②分点P在直线AB上方和直线AB下方两种情况讨论,由全等三角形的性质和等腰三角形的性质可求解.
解:(1)∵△ABC是等边三角形,
∴∠CAB=∠CBA=60°,AC=CB=AB,且PC⊥AB,
∴PC垂直平分AB,
∴PA=PB,且∠APB=α,PC⊥AB,
∴∠APC=∠BPC=![]() α,
α,
∴∠PAB=∠PBA=90°﹣![]() ,
,
∴∠PAC=∠PAB+∠BAC=150°﹣![]() ;
;
(2)①△ADP是等边三角形,
理由如下:∵∠PAD=60°=∠CAB,
∴∠DAB=∠PAC,
∵△ABC是等边三角形,CP⊥AB,
∴∠ACP=∠BCP=30°,
∵DB⊥BC,∠ABC=60°
∴∠DBA=30°=∠ACP,且AC=AB,∠DAB=∠PAC,
∴△DAB≌△PAC(ASA)
∴AD=AP,且∠DAP=60°,
∴△ADP是等边三角形;
②如图3,点P在AB上方时,
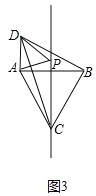
∵CD=![]() AB.
AB.
∴CD=![]() BC,
BC,
∵∠DBC=90°,
∴CD2=DB2+BC2,
∴BC=DB,
∴AB=DB,且∠DBA=30°,
∴∠ADB=75°,
∵△DAB≌△PAC,
∴∠APC=∠ADB=75°,
∴α=150°;
如图4,点P在AB下方时,
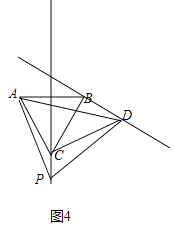
∵DB⊥BC,∠ABC=60°
∴∠ABD=150°
∵CD=![]() AB.
AB.
∴CD=![]() BC,
BC,
∵∠DBC=90°,
∴CD2=DB2+BC2,
∴BC=DB,
∴AB=DB,且∠ABD=150°,
∴∠ADB=15°,
∵∠PAD=60°=∠CAB,
∴∠DAB=∠PAC,
∵△ABC是等边三角形,CP⊥AB,
∴∠ACP=∠BCP=180°﹣30°=150°,
∴∠DBA=150°=∠ACP,且AC=AB,∠DAB=∠PAC,
∴△DAB≌△PAC(SAS)
∴∠APC=∠ADB=15°,
∴α=30°,


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研其性质——运用函数解决问题”的学习过程.如图,在平面直角坐标系中己经绘制了一条直线![]() .另一函数
.另一函数![]() 与
与![]() 的函数关系如下表:
的函数关系如下表:
| … | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … | -2 | -0.25 | 1 | 1.75 | 2 | 1.75 | 1 | -0.25 | -2 | -4.25 | -7 | -10.25 | -14 | … |
(1)求直线![]() 的解析式;
的解析式;
(2)请根据列表中的数据,绘制出函数![]() 的近似图像;
的近似图像;
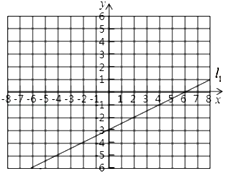
(3)请根据所学知识并结合上述信息拟合出函数![]() 的解折式,并求出
的解折式,并求出![]() 与
与![]() 的交点坐标.
的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
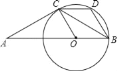
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以O为圆心,OB为半径作圆,过C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)已知AC=6,求扇形OBC围成的圆锥的底面圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过点
的图像经过点![]() (1,0).
(1,0).
(1)当![]() ,
,![]() 时,求二次函数的解析式及二次函数最小值;
时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图像经过点![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ).若对任意实数
).若对任意实数![]() ,函数值
,函数值![]() 都不小于
都不小于![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
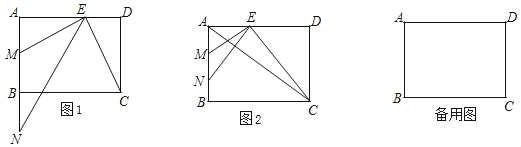
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
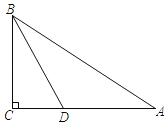
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com