
【题目】△ABC为等边三角形,![]() .
.![]() .
.
(1)求证:四边形![]() 是菱形.
是菱形.
(2)若![]() 是
是![]() 的角平分线,连接
的角平分线,连接![]() ,找出图中所有的等腰三角形.
,找出图中所有的等腰三角形.
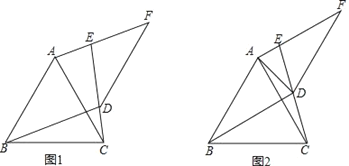
【答案】(1)证明见解析;(2)图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.
【解析】
(1)先求证BD∥AF,证明四边形ABDF是平行四边形,再利用有一组邻边相等的平行四边形是菱形即可证明;(2)先利用BD平分∠ABC,得到BD垂直平分线段AC,进而证明△DAC是等腰三角形,根据BD⊥AC,AF⊥AC,找到角度之间的关系,证明△DAE是等腰三角形,进而得到BC=BD=BA=AF=DF,即可解题,见详解.
(1)如图1中,∵∠BCD=∠BDC,
∴BC=BD,
∵△ABC是等边三角形,
∴AB=BC,
∵AB=AF,
∴BD=AF,
∵∠BDC=∠AEC,
∴BD∥AF,
∴四边形ABDF是平行四边形,
∵AB=AF,
∴四边形ABDF是菱形.
(2)解:如图2中,∵BA=BC,BD平分∠ABC,
∴BD垂直平分线段AC,
∴DA=DC,
∴△DAC是等腰三角形,
∵AF∥BD,BD⊥AC
∴AF⊥AC,
∴∠EAC=90°,
∵∠DAC=∠DCA,∠DAC+∠DAE=90°,∠DCA+∠AEC=90°,
∴∠DAE=∠DEA,
∴DA=DE,
∴△DAE是等腰三角形,
∵BC=BD=BA=AF=DF,
∴△BCD,△ABD,△ADF都是等腰三角形,
综上所述,图中等腰三角形有△ABC,△BDC,△ABD,△ADF,△ADC,△ADE.


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
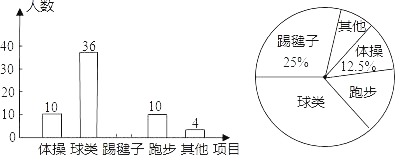
【题目】为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
(1)补全频数分布直方图;
(2)求扇形统计图中表示“踢毽子”项目扇形圆心角的度数.
(3)估计该校1800名学生中有多少人最喜爱球类活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
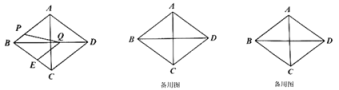
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,则下列结论正确的有( )个.
,则下列结论正确的有( )个.
(1)![]() (2)
(2)![]()
(3)![]() 的面积是18 (4)
的面积是18 (4)![]()

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度是
方向匀速运动,速度是![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度是
方向匀速运动,速度是![]() ,
,![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .设运动时间为
.设运动时间为![]() .
.
(1)当![]() 于
于![]() 时,求
时,求![]() 的值;
的值;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻![]() ,使
,使![]() 平分
平分![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】明朝的数学家程大位在《算法统宗》中有一道古诗趣题:甲赶群羊逐草茂,乙拽只羊随其后,戏问甲及一百否?甲云所曰无差谬;若得这般一群羊,再添半群小半群,得你一只来方凑,玄机妙算谁猜透?其大意是:甲赶一群羊去放,乙也牵着一只羊跟在甲的后面.乙问甲:“你的这群羊有没有一百只呢?”甲说:“我再得这样的一群羊,再得这群羊的一半,还得这群羊的四分之一,最后凑上你的这只羊,正好是一百只.”问甲原有多少只羊?设甲原有x只羊,根据题意,可列方程为_________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
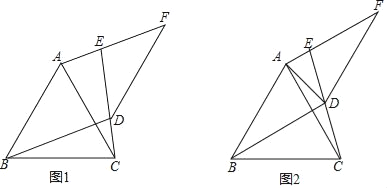
【题目】如图1,菱形![]() 中,
中,![]() ,
,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
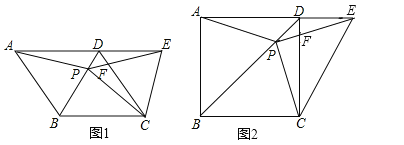
(1)证明:![]() ;
;
(2)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)如图2,把菱形![]() 改为正方形
改为正方形![]() ,其他条件不变,直接写出线段
,其他条件不变,直接写出线段![]() 与线段
与线段![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com