
【题目】如图,∠AOB=25°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为( )
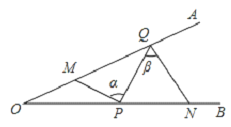
A.50°B.40°C.30°D.25°
【答案】B
【解析】
如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,根据三角形的外角的性质和平角的定义即可得到结论.
解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
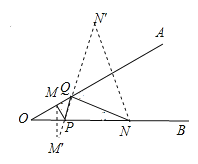
∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∴∠QPN=![]() (180°-α)=∠AOB+∠MQP=20°+
(180°-α)=∠AOB+∠MQP=20°+![]() (180°-β),
(180°-β),
∴180°-α=40°+(180°-β),
∴β-α=40°,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,直线l∥AB,P是直线l上一动点.对于下列各值:①线段AB的长②△PAB的周长③△PAB的面积④∠APB的度数其中不会随点P的移动而变化的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的纸片,长AD=10厘米,宽AB=8厘米,AD沿点A对折,点D正好落在BC上的点F处,AE是折痕.
(1)图中有全等的三角形吗?如果有,请直接写出来;
(2)求线段EF的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2).点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2016次相遇时的坐标为_____.
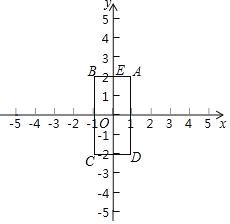
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点的坐标分别为(﹣2,2)、(1,8).

(1)求三角形ABO的面积;
(2)若y轴上有一点M,且三角形MAB的面积为10,求M点的坐标;
(3)如图,把直线AB以每秒2个单位的速度向右平移,问经过多少秒后,该直线与y轴交于点(0,﹣2)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() c为常数
c为常数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() ,顶点为点M,过点A作
,顶点为点M,过点A作![]() 轴,交y轴于点D,交该二次函数图象于点B,连结BC.
轴,交y轴于点D,交该二次函数图象于点B,连结BC.
![]() 求该二次函数的解析式及点M的坐标.
求该二次函数的解析式及点M的坐标.
![]() 过该二次函数图象上一点P作y轴的平行线,交
过该二次函数图象上一点P作y轴的平行线,交![]() 一边于点Q,是否存在点P,使得以点P、Q、C、O为顶点的四边形为平行四边形,若存在,求出P点坐标;若不存在,说明理由.
一边于点Q,是否存在点P,使得以点P、Q、C、O为顶点的四边形为平行四边形,若存在,求出P点坐标;若不存在,说明理由.
![]() 点N是射线CA上的动点,若点M、C、N所构成的三角形与
点N是射线CA上的动点,若点M、C、N所构成的三角形与![]() 相似,请直接写出所有点N的坐标
相似,请直接写出所有点N的坐标![]() 直接写出结果,不必写解答过程
直接写出结果,不必写解答过程![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→)(0,1)→(0,2)→……,且每秒移动一个单位,那么第2018秒时,点所在位置的坐标是( ).

A. (6,44)B. (38,44)C. (44,38)D. (44,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
1×2×3×4+1=________;
2×3×4×5+1=_______;
3×4×5×6+1=_______;
4×5×6×7+1=________;
(2)观察上述计算的结果,指出他们的共同特性;
(3)以上特性,对于任意给出的四个连续自然数的积与1的和仍具备吗?试证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com