
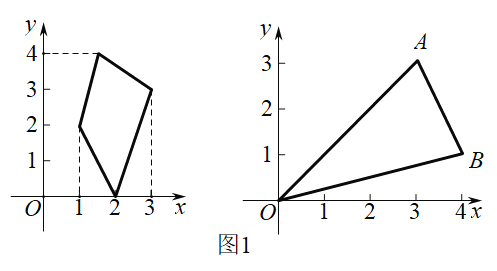
【题目】在平面直角坐标系xOy中,图形W在坐标轴上的投影长度定义如下:
设点P![]() ,Q
,Q![]() 是图形W上的任意两点.若
是图形W上的任意两点.若![]() 的最大值为m,则图形W在x轴上的投影长度
的最大值为m,则图形W在x轴上的投影长度![]() =m;若
=m;若![]() 的最大值为n,则图形W在y轴上的投影长度
的最大值为n,则图形W在y轴上的投影长度![]() =n,如下图,图形W在x轴上的投影长度
=n,如下图,图形W在x轴上的投影长度![]() =
=![]() =2;在y轴上的投影长度
=2;在y轴上的投影长度![]() =
=![]() =4.
=4.
(1)已知点A(3,3),B(4,1).如图1所示,若图形W为△OAB,则![]() =___________
=___________ ![]() =___________
=___________
(2)已知点C(4,0),点D在直线y=-2x+6上,若图形W为△OCD.当=![]() 时,求点D的坐标.
时,求点D的坐标.
(3)如图2所示,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD,BD.若图形W为点O.A.C.D.B围成的多边形图象,且∠DOA=∠OBA,直接写出![]() 的值
的值
【答案】(1)![]() ;(2)点D的坐标为(1,4)或(6,-6),(3)
;(2)点D的坐标为(1,4)或(6,-6),(3)![]() 或
或![]()
【解析】
(1)确定出点A在y轴的投影的坐标、点B在x轴上投影的坐标,于是可求得问题的答案;
(2)过点P作PD⊥x轴,垂足为P.设D(x,-2x+6),则PD=|-2x+6|.PC=|4-x|,然后依据![]() ,列方程求解即可.
,列方程求解即可.
(3)分情况讨论,当D在第一象限时,由旋转的性质结合∠DOA=∠OBA,证明![]() 三点共线,过C作CF
三点共线,过C作CF![]() OB于F,过C作CG
OB于F,过C作CG![]() OA于G,设
OA于G,设![]() 利用勾股定理列出方程组即可得到答案.当D在第四象限时,过D作DF
利用勾股定理列出方程组即可得到答案.当D在第四象限时,过D作DF![]() OB于F,过D作DG
OB于F,过D作DG![]() OA于G,则四边形
OA于G,则四边形![]() 为矩形,设
为矩形,设![]() 建立方程组求解即可.
建立方程组求解即可.
解:(1)∵A(3,3),
∴点A在y轴上的正投影的坐标为(0,3).
∴△OAB在y轴上的投影长度![]() .
.
∵B(4,1),
∴点B在x轴上的正投影的坐标为(4,0).
∴△OAB在x轴上的投影长度![]() .
.
故答案为:4,3.
(2)如图1所示;过点P作PD⊥x轴,垂足为P.
0≤x≤3时,-2x+6=4, 解得x=1.
∴D(1,4).
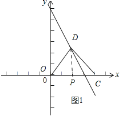
如图2所示:过点D作DP⊥x轴,垂足为P.
当3<x≤4时,
所以2x-6=4,
解得:x=5(舍去),
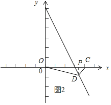
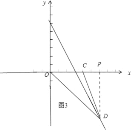
如图3所示,当点D在C点右侧,x>4时,
x=2x-6, 可得x=6 ,
点D坐标(6,-6),
如图4所示:当 x<0时,-2x+6=4-x,
解得:x=2 舍去,
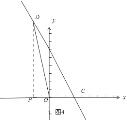
综上所述,点D的坐标为(1,4)或(6,-6).
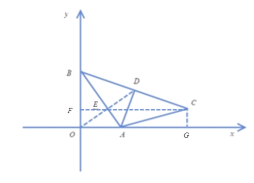
(3)如图,当D在第一象限时,
![]() ∠DOA=∠OBA,
∠DOA=∠OBA,
![]()
![]()
![]()
由旋转可知:![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]()
![]() 三点共线,
三点共线,![]()
过C作CF![]() OB于F,过C作CG
OB于F,过C作CG![]() OA于G,
OA于G,
则四边形![]() 为矩形,
为矩形,
设![]()
![]()
![]()
![]()
由勾股定理得:
消去![]() 得:
得:![]()
![]()
![]() (舍去)
(舍去)
![]()
![]()
如下图,当点C旋转到![]() 轴的负半轴上,D在第四象限时,
轴的负半轴上,D在第四象限时,
![]()
![]()
同理可得:![]() 是
是![]() 的垂直平分线,
的垂直平分线,
过D作DF![]() OB于F,过D作DG
OB于F,过D作DG![]() OA于G,
OA于G,
则四边形![]() 为矩形,
为矩形,
设![]()
同理可得:
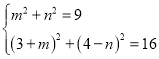
消去![]() 得:
得:![]()
![]()
![]() (舍去)
(舍去)
![]()
此时:![]()
综上:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6.…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0).则依图中所示规律,A2020的坐标为( )
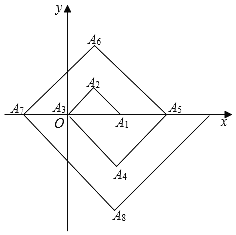
A.(2,﹣1010)B.(2,﹣1008)C.(1010,0)D.(1,1009)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,AB=CD,∠A=∠D.
(1)求证:四边形ABCD为矩形
(2)若点E是AB边上的中点,点F为AD边上一点,∠1=2∠2,CF=5,求AF+BC的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①AB//CD;②AB=CD;③BC//AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有哪几种,请一一写出_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】好邻居超市购进一批面粉,标准质量为![]() ,现抽取
,现抽取![]() 袋样品进行称重检测,为记录的方便,用“
袋样品进行称重检测,为记录的方便,用“![]() ”表示超过标准的重量,用“
”表示超过标准的重量,用“![]() ”表示不足标准的重量,结果如下表(单位
”表示不足标准的重量,结果如下表(单位![]() ):
):
与标准差( |
|
|
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
| 3 |
(1)求这![]() 袋样品超出或不足的质量为多少?
袋样品超出或不足的质量为多少?
(2)这批面粉的总重量为多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣4,0)、B(1,0)、C(0,3)三点,直线y=mx+n经过A(﹣4,0)、C(0,3)两点.
(1)写出方程ax2+bx+c=0的解;
(2)若ax2+bx+c>mx+n,写出x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com