
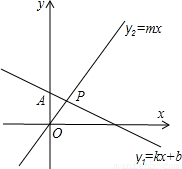
 (2010•武汉)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 .
(2010•武汉)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 .  名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源:2011年安徽省安庆市桐城二中中考数学一模试卷(解析版) 题型:填空题
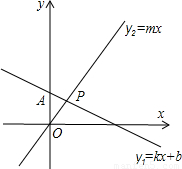 (2010•武汉)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 .
(2010•武汉)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 .查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
 )两点,与x轴交于另一点B.
)两点,与x轴交于另一点B. y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;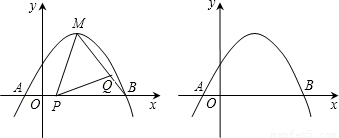
查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市中考数学试卷(解析版) 题型:解答题
 )两点,与x轴交于另一点B.
)两点,与x轴交于另一点B.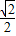 y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市中考数学试卷(解析版) 题型:填空题
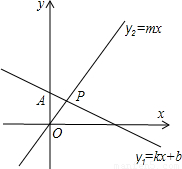 (2010•武汉)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 .
(2010•武汉)如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com