
ЁОЬтФПЁПвбжЊЃКдкЁїABCжаЃЌAB=ACЃЌDЪЧBCЕФжаЕуЃЌЖЏЕуEдкБпABЩЯЃЈЕуEВЛгыЕуAЃЌBжиКЯЃЉ, ЖЏЕуFдкЩфЯпACЩЯЃЌСЌНсDE, DF.
(1)ШчЭМ1ЃЌЕБЁЯDEB=ЁЯDFC=90ЁуЪБЃЌжБНгаДГіDEгыDFЕФЪ§СПЙиЯЕ;

(2)ШчЭМ2ЃЌЕБЁЯDEB+ЁЯDFC=180Ёу(ЁЯDEBЁйЁЯDFC)ЪБЃЌВТЯыDEгыDFЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЛ

(3)ЕБЕуE,D,FдкЭЌвЛЬѕжБЯпЩЯЪБЃЌ
ЂйвРЬтвтВЙШЋЭМ3ЃЛ
ЂкдкЕуEдЫЖЏЕФЙ§ГЬжаЃЌЪЧЗёДцдкEB=FCЃП ЃЈ ЬюЁАДцдкЁБЛђЁАВЛДцдкЁБ ЃЉ.

ЁОД№АИЁПЃЈ1ЃЉDE=DFЃЛЃЈ2ЃЉDE=DFЃЛжЄУїМћНтЮіЃЛЃЈ3ЃЉЂйМћНтЮіЃЌЂкВЛДцдк
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїЁїBEDЁеЁїCFDЃЌРћгУШЋЕШШ§НЧаЮЕФЖдгІБпЯрЕШМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉСЌНгADЃЌзїDGЁЭABгкЕуGЃЌDHЁЭACгкЕуHЃЌИљОнЭЌНЧЕФВЙНЧЯрЕШЃЌЕУГіЁЯGED=ЁЯDFCЃЌИљОнЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪЕУЕНЁЯBAD=ЁЯCADЃЌдйИљОнНЧЦНЗжЯпЕФаджЪЕУГіDG=DHЃЌМДПЩжЄУїЁїEGDЁеЁїFHDЃЌДгЖјЕУГіНсТлЃЛ
ЃЈ3ЃЉЂйИљОнЬтвтВЙШЋЭМаЮМДПЩЃЛ
ЂкМйЩшBE=CFЃЎЙ§EзїEGЁЮACНЛBCгкGЃЎжЄУїЁїEGDЁеЁїFCDЃЌЕУЕНGD=CDЃЌНјЖјЕУЕНGгыBжиКЯЃЎгЩBEгыACЯрНЛгкЕуAЃЌгыEGЁЮACУЌЖмЃЌЕУГіBE=CFВЛГЩСЂЃЌДгЖјЕУЕННсТлЃЎ
ЃЈ1ЃЉDEгыDFЕФЪ§СПЙиЯЕЪЧDE=DFЃЎРэгЩШчЯТЃК
ЁпAB=ACЃЌЁрЁЯB=ЁЯCЃЎ
ЁпDЪЧBCЕФжаЕуЃЌЁрBD=CDЃЎ
дкЁїBEDКЭЁїCFDжаЃЌЁпЁЯB=ЁЯCЃЌЁЯDEB=ЁЯDFC=90ЁуЃЌBD=CDЃЌ
ЁрЁїBEDЁеЁїCFDЃЈAASЃЉЃЌ
ЁрDE=DFЃЎ
ЃЈ2ЃЉВТЯыЃКDEгыDFЕФЪ§СПЙиЯЕЪЧDE=DFЃЎРэгЩШчЯТЃК
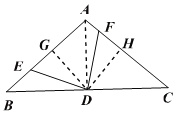
СЌНгADЃЌзїDGЁЭABгкЕуGЃЌDHЁЭACгкЕуHЃЌ
ЁрЁЯEGD=ЁЯFHD=90ЁуЃЎ
ЁпЁЯDEB+ЁЯGED=180ЁуЃЌ
ЁЯDEB+ЁЯDFC=180ЁуЃЌ
ЁрЁЯGED=ЁЯDFCЃЎ
ЁпAB=ACЃЌDЪЧBCЕФжаЕуЃЌ
ЁрЁЯBAD=ЁЯCADЃЎ
ЁпDGЁЭABЃЌDHЁЭACЃЌ
ЁрDG=DHЃЎ
дкЁїEGDКЭЁїFHDжаЃЌ
Ёп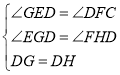 ЃЌ
ЃЌ
ЁрЁїEGDЁеЁїFHDЃЌ
ЁрDE=DFЃЎ
ЃЈ3ЃЉЂйзїЭМШчЯТЃК
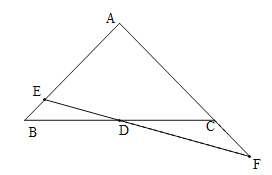
ЂкВЛДцдкЃЎРэгЩШчЯТЃК
МйЩшBE=CFЃЎЙ§EзїEGЁЮACНЛBCгкGЃЎ
ЁпEGЁЮACЃЌЁрЁЯEGB=ЁЯACBЃЌЁЯEGD=ЁЯFCDЃЎ
ЁпAB=ACЃЌЁрЁЯB=ЁЯACBЃЌ
ЁрЁЯB=ЁЯEGBЃЌ
ЁрBE=EGЃЎ
ЁпBE=CFЃЌ
ЁрEG=CFЃЎ
дкЁїEGDКЭЁїFCDжаЃЌ
ЁпЁЯEGD=ЁЯFCDЃЌЁЯEDG=ЁЯFDCЃЌEG=FCЃЌ
ЁрЁїEGDЁеЁїFCDЃЌ
ЁрGD=CDЃЎ
ЁпBD=CDЃЌ
ЁрBD=GDЃЌ
ЁрGгыBжиКЯЃЎ
ЁпBEгыACЯрНЛгкЕуAЃЌгыEGЁЮACУЌЖмЃЌ
ЁрBE=CFВЛГЩСЂЃЌ
ЁрдкЕуEдЫЖЏЕФЙ§ГЬжаЃЌВЛДцдкEB=FCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=x2Љ4x+3ЃЎ
ЃЈ1ЃЉгУХфЗНЗЈНЋДЫЖўДЮКЏЪ§ЛЏЮЊЖЅЕуЪНЃЛ
ЃЈ2ЃЉЧѓГіЫќЕФЖЅЕузјБъКЭЖдГЦжсЃЛ
ЃЈ3ЃЉЧѓГіЖўДЮКЏЪ§ЕФЭМЯѓгыxжсЕФСНИіНЛЕузјБъЃЛ
ЃЈ4ЃЉдкЫљИјЕФзјБъЯЕЩЯЃЌЛГіетИіЖўДЮКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ5ЃЉЙлВьЭМЯѓЬюПеЃЌЪЙyЫцxЕФдіДѓЖјМѕаЁЕФxЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPЪЧСтаЮABCDБпЩЯЕФвЛЖЏЕуЃЌЫќДгЕуAГіЗЂбидкAЁњBЁњCЁњDТЗОЖдШЫйдЫЖЏЕНЕуDЃЌЩшЁїPADЕФУцЛ§ЮЊyЃЌPЕуЕФдЫЖЏЪБМфЮЊxЃЌдђyЙигкxЕФКЏЪ§ЭМЯѓДѓжТЮЊЃЈЁЁЁЁЃЉ

A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊyЪЧx ЕФКЏЪ§ЃЌздБфСПxЕФШЁжЕЗЖЮЇЪЧx >0ЃЌЯТБэЪЧyгыx ЕФМИзщЖдгІжЕ.
x | ЁЄЁЄЁЄ | 1 | 2 | 3 | 5 | 7 | 9 | ЁЄЁЄЁЄ |
y | ЁЄЁЄЁЄ | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ЁЄЁЄЁЄ |
аЁЬкИљОнбЇЯАвЛДЮКЏЪ§ЕФОбщЃЌРћгУЩЯЪіБэИёЫљЗДгГГіЕФyгыxжЎМфЕФБфЛЏЙцТЩЃЌЖдИУКЏЪ§ЕФЭМЯѓгыаджЪНјааСЫЬНОП.
ЯТУцЪЧаЁЬкЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕу.ИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓ;
жаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕу.ИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓ;

ЃЈ2ЃЉИљОнЛГіЕФКЏЪ§ЭМЯѓЃЌаДГіЃК
Ђйx=4ЖдгІЕФКЏЪ§жЕyдМЮЊ________ЃЛ
ЂкИУКЏЪ§ЕФвЛЬѕаджЪЃК__________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШєвЛИіШ§НЧаЮжаЃЌЦфжагавЛИіФкНЧЪЧСэЭтвЛИіФкНЧЕФвЛАыЃЌдђетбљЕФШ§НЧаЮНазіЁААыНЧШ§НЧаЮЁБ. Р§ШчЃКЕШбќжБНЧШ§НЧаЮОЭЪЧЁААыНЧШ§НЧаЮЁБ.дкЖлНЧШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() НЛ
НЛ![]() БпгкЕу
БпгкЕу![]() ЃЎЕу
ЃЎЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() бгГЄЯпЩЯЃЎ
бгГЄЯпЩЯЃЎ


Ђй ЕБ![]() ЃЌЕу
ЃЌЕу![]() ЧЁКУЮЊ
ЧЁКУЮЊ![]() жаЕуЪБЃЌвРОнЬтвтВЙШЋЭМ1.ЧыаДГіЭМжаЕФвЛИіЁААыНЧШ§НЧаЮЁБЃК_______;
жаЕуЪБЃЌвРОнЬтвтВЙШЋЭМ1.ЧыаДГіЭМжаЕФвЛИіЁААыНЧШ§НЧаЮЁБЃК_______;
Ђк ШчЭМ2ЃЌШє![]() ЃЌЭМжаЪЧЗёДцдкЁААыНЧШ§НЧаЮЁБЃЈЁї
ЃЌЭМжаЪЧЗёДцдкЁААыНЧШ§НЧаЮЁБЃЈЁї![]() Г§ЭтЃЉЃЌШєДцдкЃЌЧыаДГіЭМжаЕФЁААыНЧШ§НЧаЮЁБЃЌВЂжЄУїЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
Г§ЭтЃЉЃЌШєДцдкЃЌЧыаДГіЭМжаЕФЁААыНЧШ§НЧаЮЁБЃЌВЂжЄУїЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌШє![]() ЃЌБЃГж
ЃЌБЃГж![]() ЕФЖШЪ§гыЃЈ1ЃЉжаЂкЕФНсТлЯрЭЌЃЌЧыжБНгаДГі
ЕФЖШЪ§гыЃЈ1ЃЉжаЂкЕФНсТлЯрЭЌЃЌЧыжБНгаДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ТњзуЕФЪ§СПЙиЯЕЃК______ЃЎ
ТњзуЕФЪ§СПЙиЯЕЃК______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊГЃЪ§ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌЯТСа
ЮЊГЃЪ§ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌЯТСа![]() ИіНсТлЃКЂй
ИіНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЮЊГЃЪ§ЃЌЧв
ЮЊГЃЪ§ЃЌЧв![]() ЃЎЦфжае§ШЗЕФНсТлгаЃЈ ЃЉ
ЃЎЦфжае§ШЗЕФНсТлгаЃЈ ЃЉ
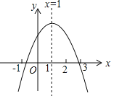
A. 2Иі B. 3Иі C. 4Иі D. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAдкжБЯпlЩЯЃЌЕуBдкжБЯпlЭтЃЌЕуBЙигкжБЯпlЕФЖдГЦЕуЮЊCЃЌСЌНгACЃЌЙ§ЕуBзїBDЁЭACгкЕуDЃЌбгГЄBDжСEЪЙBE=ABЃЌСЌНгAEВЂбгГЄгыBCЕФбгГЄЯпНЛгкЕуF.

ЃЈ1ЃЉВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉШєЁЯBAC=2ІСЃЌЧѓГіЁЯAEBЕФДѓаЁЃЈгУКЌІСЕФЪНзгБэЪОЃЉЃЛ
ЃЈ3ЃЉгУЕШЪНБэЪОЯпЖЮEFгыBCЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃМЦЛЎДгЩЬЕъЙКНј![]() СНжжЩЬЦЗЃЌЙКТђвЛИі
СНжжЩЬЦЗЃЌЙКТђвЛИі![]() ЩЬЦЗБШЙКТђвЛИі
ЩЬЦЗБШЙКТђвЛИі![]() ЩЬЦЗЖрЛЈ10дЊЃЌВЂЧвЛЈЗб300дЊЙКТђ
ЩЬЦЗЖрЛЈ10дЊЃЌВЂЧвЛЈЗб300дЊЙКТђ![]() ЩЬЦЗКЭЛЈЗб100дЊЙКТђ
ЩЬЦЗКЭЛЈЗб100дЊЙКТђ![]() ЩЬЦЗЕФЪ§СПЯрЕШ.
ЩЬЦЗЕФЪ§СПЯрЕШ.
ЃЈ1ЃЉЧѓЙКТђвЛИі![]() ЩЬЦЗКЭвЛИі
ЩЬЦЗКЭвЛИі![]() ЩЬЦЗИїашвЊЖрЩйдЊЃЛ
ЩЬЦЗИїашвЊЖрЩйдЊЃЛ
ЃЈ2ЃЉИљОнбЇаЃЪЕМЪЧщПіЃЌИУбЇаЃашвЊЙКТђ![]() жжЩЬЦЗЕФИіЪ§ЪЧЙКТђ
жжЩЬЦЗЕФИіЪ§ЪЧЙКТђ![]() жжЩЬЦЗИіЪ§ЕФ3БЖЃЌЛЙЖр11ИіЃЌОгыЩЬЕъЧЂЬИЃЌЩЬЕъОіЖЈдкИУбЇаЃЙКТђ
жжЩЬЦЗИіЪ§ЕФ3БЖЃЌЛЙЖр11ИіЃЌОгыЩЬЕъЧЂЬИЃЌЩЬЕъОіЖЈдкИУбЇаЃЙКТђ![]() жжЩЬЦЗЪБИјгшАЫелгХЛнЃЌШчЙћИУбЇаЃБОДЮЙКТђ
жжЩЬЦЗЪБИјгшАЫелгХЛнЃЌШчЙћИУбЇаЃБОДЮЙКТђ![]() СНжжЩЬЦЗЕФзмЗбгУВЛГЌЙ§1000дЊЃЌФЧУДИУбЇаЃзюЖрПЩЙКТђЖрЩйИі
СНжжЩЬЦЗЕФзмЗбгУВЛГЌЙ§1000дЊЃЌФЧУДИУбЇаЃзюЖрПЩЙКТђЖрЩйИі![]() жжЩЬЦЗЃП
жжЩЬЦЗЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕШбќ![]() жаЃЌ
жаЃЌ![]() ЪЧBCБпЩЯЕФИпЃЌЧв
ЪЧBCБпЩЯЕФИпЃЌЧв![]() ЃЌдђЕШбќ
ЃЌдђЕШбќ![]() ЕзНЧЕФЖШЪ§ЮЊ__________.
ЕзНЧЕФЖШЪ§ЮЊ__________.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com