
分析 分k=0和k≠0两种情况考虑.当k=0时可求出x的值,从而得出k=0符合题意;当k≠0时,由方程有解结合根的判别式即可得出△=-(3k2-1)(k2+1)≥0,由此可得出3k2-1≤0,结合k为整数且非零可知该不等式无解.综上即可得出结论.
解答 解:当k=0时,有x+1=0,
解得:x=-1,
∴k=0符合题意;
当k≠0时,关于x的方程k2x2-(k+1)2x+k2+1=0为一元二次方程,
∵关于x的方程k2x2-(k+1)2x+k2+1=0有实数根,
∴△=(k+1)4-4k2(k2+1)=-3k4-2k2+1=-(3k2-1)(k2+1)≥0,
∴3k2-1≤0,k2+1≥0,
∴k2$≤\frac{1}{3}$,
∵k为整数,且k≠0,
∴不等式k2$≤\frac{1}{3}$无解.
综上所述:整数k的值为0.
点评 本题考查了根的判别式、解一元一次方程以及一元二次不等式,解题的关键是分k=0和k≠0两种情况考虑.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等腰三角形,∠BAC=90°,D为BC延长线上一点,连续AD,以AD为边在AD右侧作正方形ADEF,连续FC、EC,若AC=$\sqrt{2}$,AD=$\sqrt{10}$.
如图,△ABC是等腰三角形,∠BAC=90°,D为BC延长线上一点,连续AD,以AD为边在AD右侧作正方形ADEF,连续FC、EC,若AC=$\sqrt{2}$,AD=$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
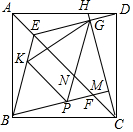 如图,四边形ABCD为正方形,H是AD上任意一点,连接CH,过B作BM⊥CH于M,交AC于F,过D作DE∥BM交AC于E,交CH于G,在线段BF上作PF=DG,连接PG,BE,其中PG交AC于N点,K为BE上一点,连接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求$\frac{KG}{EG}$的值为$\frac{\sqrt{505}}{15}$.
如图,四边形ABCD为正方形,H是AD上任意一点,连接CH,过B作BM⊥CH于M,交AC于F,过D作DE∥BM交AC于E,交CH于G,在线段BF上作PF=DG,连接PG,BE,其中PG交AC于N点,K为BE上一点,连接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求$\frac{KG}{EG}$的值为$\frac{\sqrt{505}}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
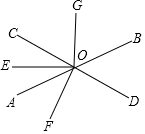 如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
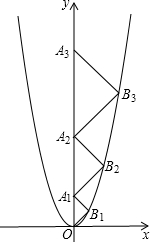 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com