
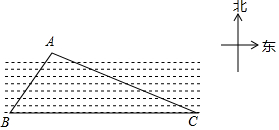
 如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为20$\sqrt{3}$米.
如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为20$\sqrt{3}$米. 分析 方法1、作AD⊥BC于点D,设出AD=x米,在Rt△ACD中,得出CD=$\sqrt{3}$x,在Rt△ABD中,得出BD=$\frac{\sqrt{3}}{3}$x,最后用CD+BD=80建立方程即可得出结论;
方法2、先判断出△ABC是直角三角形,利用含30°的直角三角形的性质得出AB,AC,再利用同一个直角三角形,两直角边的积的一半和斜边乘以斜边上的高的一半建立方程求解即可.
解答 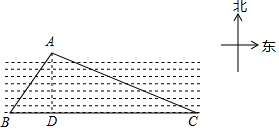 解:方法1、过点A作AD⊥BC于点D.
解:方法1、过点A作AD⊥BC于点D.
根据题意,∠ABC=90°-30°=60°,∠ACD=30°,
设AD=x米,
在Rt△ACD中,tan∠ACD=$\frac{AD}{CD}$,
∴CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{tan30°}$=$\sqrt{3}$x,
在Rt△ABD中,tan∠ABC=$\frac{AD}{BD}$,
∴BD=$\frac{AD}{tan∠ABC}$=$\frac{x}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
∴BC=CD+BD=$\sqrt{3}$x+$\frac{\sqrt{3}}{3}$x=80
∴x=20$\sqrt{3}$
答:该河段的宽度为20$\sqrt{3}$米.
故答案是:20$\sqrt{3}$米.
方法2、过点A作AD⊥BC于点D.
根据题意,∠ABC=90°-30°=60°,∠ACD=30°,
∴∠BAC=180°-∠ABC-∠ACB=90°,
在Rt△ABC中,BC=80m,∠ACB=30°,
∴AB=40m,AC=40$\sqrt{3}$m,
∴S△ABC=$\frac{1}{2}$AB×AC=$\frac{1}{2}$×40×40$\sqrt{3}$=800$\sqrt{3}$,
∵S△ABC=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×80×AD=40AD=800$\sqrt{3}$,
∴AD=20$\sqrt{3}$米
答:该河段的宽度为20$\sqrt{3}$米.
故答案是:20$\sqrt{3}$米.
点评 此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角.


科目:初中数学 来源: 题型:选择题
| A. | m≤-1 | B. | m<-1 | C. | -1<m≤0 | D. | -1≤m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
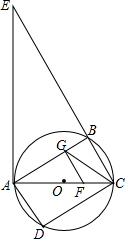 如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.
如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
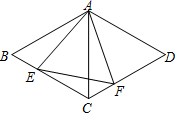 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )| A. | $4\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com