练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长是
     
    ．
    考点：圆的认识,勾股定理
    专题：
    分析：先连接OC，在Rt△ODC中，根据勾股定理得出OC的长，即可求出AB的长．
    解答：解：连接OC，
    ∵CD=4，OD=3，
    在Rt△ODC中，
    ∴OC=
    		OD2+CD2
    =
    		32+42
    =5，
    ∴AB=2OC=10，
    故答案为：10．
    点评：此题考查了圆的认识，解题的关键是根据勾股定理求出圆的半径，此题较简单．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知p，q均为质数，且满足7p2+3q=79，则p=
     
    ，q=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

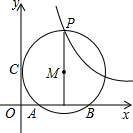    平面直角坐标系中，半径为5的⊙M与x轴交于A、B两点，且AB=8，与y轴切于点C，若双曲线y=
    k
    x
    正好经过AB的垂直平分线与⊙M的交点P，则k=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    为提高技术工人的技能技巧，某石油分公司举办了一期岗位培训班．培训结业时出了如下一道试题：有一油罐，其直径为6米，高为8米，如图，将一长为12米的金属棒置于其中，假如金属棒露在外面的长为h米，试问h的取值范围是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若30030的质因数的（算术）平均数为M，则与M最接近的整数是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a，b是实数，x=a2+b2+20，y=4（2b-a），则x、y的大小关系是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a＞b，则下列结论正确的是（　　）
    A、a2＞b2
    B、a3＞b3
    C、
    1
    a
    ＜
    1
    b
    D、
    a
    b
    ＞1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    教育部制订《全日制义务教育•数学课程标准》要求：面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻求解决问题的策略．
    某零件厂为降低成本，减小损耗，打算把一种废弃的圆形铁片加工成小零件，现需要确定这个圆形铁片的圆心，请你运用所学数学知识，至少提供三个方案，简述设计思路及过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若n是正整数，且x2n=5，则（2x3n）2÷（4x2n）=
     
    ．

    查看答案和解析>>

    同步练习册答案