
分析 根据有理数的分类即可填写,有理数$\left\{\begin{array}{l}{整数\left\{\begin{array}{l}{正整数}\\{0}\\{负整数}\end{array}\right.}\\{分数\left\{\begin{array}{l}{正分数}\\{负分数}\end{array}\right.}\end{array}\right.$.
解答 解:(1)正数集合:{|-$\frac{3}{7}$|,+2.97,-(-5),$\frac{1}{3}$…}
(2)负数集合:{-3,-11,-3.14…}
(3)整数集合:{-3,-11,0,-(-5)…}
(4)分数集合:{|-$\frac{3}{7}$|,-3.14,+2.97,$\frac{1}{3}$…}.
故答案为:(1){|-$\frac{3}{7}$|,+2.97,-(-5),$\frac{1}{3}$…};(2){-3,-11,-3.14…};(3){-3,-11,0,-(-5)…};(4){|-$\frac{3}{7}$|,-3.14,+2.97,$\frac{1}{3}$…}.
点评 此题考查了有理数,弄清有理数的分类是解本题的关键.


科目:初中数学 来源: 题型:填空题
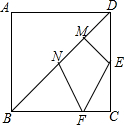 正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=$\sqrt{2}$,求四边形EMNF周长的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=$\sqrt{2}$,求四边形EMNF周长的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
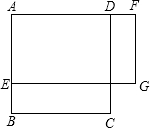 如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )| A. | y=5-x | B. | y=5-x2 | C. | y=25-x | D. | y=25-x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
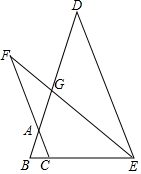 如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.
如图,在△ABC中,AB=AC,点D、E、F为三边延长线上的点,且DE∥AC,连接EF交BD于点G,∠BEF+2∠B=180°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点P,Q分别是AB,AD上的动点,则PQ+BQ的最小值是4.
如图,△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点P,Q分别是AB,AD上的动点,则PQ+BQ的最小值是4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )
如图,数轴上A,B两点表示的数分别为-1,-$\sqrt{2}$,点B关于点A的对称点为点C,则点C所表示的数是( )| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com