Question

18．如图，在矩形ABCD中，AB=6cm，BC=16cm，动点E、F同时从点A出发，点E沿A→D的方向运动，速度为每秒1cm；点F沿A→B→C的方向运动，速度为每秒2cm，当点E、F有一点到达终点时（即点E到达点D，点F到达点C），运动结束，以线段EF为边向右侧作正方形EFGH，设运动时间为t（秒）．
（1）当t为何值时，点G落在BC边上？
（2）若正方形EFGH与矩形ABCD重叠部分的面积为S（cm²），当0＜t≤8时，求S关于t的函数关系式．
（3）在点E、F运动的过程中，是否存在某一时刻t，使点D落在正方形EFGH的GH边上？若存在，请直接写出此时t的值；若不存在，请说明理由．

Answer 1

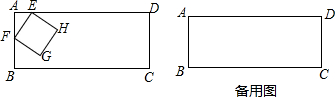
分析 （1）如图1中，当点G落在BC边上时，只要证明△AFE≌△BGF，推出AF=BG=2t．BF=AE=t，根据AB=6列出方程即可解决．
（2）分四种情形讨论：①如图2中，当0＜t≤2时，重叠部分是正方形EFGH．②如图3中，当2＜t≤3，重叠部分是五边形EFIJH．③如图4中，当3＜t≤6时，重叠部分是四边形EFJH，作EK⊥BC于点K．④如图5中，当6＜t≤8时，重叠部分是四边形EFGM，分别求出重叠部分面积即可．
（3）存在．t=3+$\sqrt{33}$．如图6中，作EK⊥BC于K，由△EFK∽△EDH，得到$\frac{EF}{ED}$=$\frac{EK}{EH}$，即EF²=EK•ED，列出方程即可解决问题．

解答 解：（1）如图1中，当点G落在BC边上时，

∵四边形EFGH是正方形，
∴EF=FG，∠EFG=90°，
∴∠AFE+∠BFG=90°，
∵∠BFG+∠BGF=90°，
∴∠AFE=∠BGF，
在△AFE和△BGF中，
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AFE=∠BGF}\\{EF=FG}\end{array}\right.$，
∴△AFE≌△BGF，
∴AF=BG=2t．BF=AE=t，
∵AF+BF=AB，
∴2t+t=6，
∴t=2，
∴当t=2秒时，点G落在BC边上．

（2）①如图2中，当0＜t≤2时，重叠部分是正方形EFGH．

∵AE=t，AF=2t，
∴S=EF²=AE²+AF²=5t²．
②如图3中，当2＜t≤3，重叠部分是五边形EFIJH．
设FG交BC于点I，GH交BC于J，则△AEFGJI∽△BFI∽△GJI，

∵AB=6，AF=2t，
∴BF=6-2t，FI=$\sqrt{5}$（6-2t）．IG=$\sqrt{5}$t-$\sqrt{5}$（6-2t）=$\sqrt{5}$（3t-6），
∴$\frac{{S}_{△GJI}}{{S}_{△AEF}}$=$\frac{I{G}^{2}}{A{F}^{2}}$=$\frac{5（3t-6）^{2}}{4{t}^{2}}$，
∴S_△GJI=$\frac{5（3t-6）^{2}}{4{t}^{2}}$•$\frac{1}{2}$•t•2t=$\frac{45}{4}$t²-45t+45，
∴S=S_{正方形EFGH}-S_△GJI=5t²-（$\frac{45}{4}$t²-45t+45）=-$\frac{25}{4}$t²+45t-45．
③当正方形EFGH的边FG落在BC上时，AE=BF，
∴t=2t-6，
∴t=6，
如图4中，当3＜t≤6时，重叠部分是四边形EFJH，作EK⊥BC于点K，

由△FJG∽△EFK，
∴$\frac{{S}_{△FJG}}{{S}_{△EFK}}$=$\frac{F{G}^{2}}{E{K}^{2}}$，
∵BF=2t-6，BK=AE=t，
∴FK=t-（2t-6）=6-t，
S_△EFK=$\frac{1}{2}$（6-t）•6=3（6-t），FG²+（6-t）²，
∴S_△FJG=$\frac{{6}^{2}+（6-t）^{2}}{{6}^{2}}$•3（6-t），
∴S=S_{正方形EFGH}-S_△FJG=6²+（6-t）²-$\frac{{6}^{2}-（6-t）^{2}}{{6}^{2}}$•3（6-t）=$\frac{1}{12}$t³-$\frac{1}{2}$t²+36．
④当点G落在CD时上，
由△EFK≌△FGC，得FC=EK=6，
∵BF=2t-6，BF+FC=BC，
∴2t-6+6=16，
∴t=8，
如图5中，当6＜t≤8时，重叠部分是四边形EFGM，

由△EMH∽△EFK，得$\frac{{S}_{△EMH}}{{S}_{△EFK}}$=$\frac{E{H}^{2}}{E{K}^{2}}$，
∵BF=2t-6，BK=AE=t，
∴KF=2t-6-t=t-6，
∴S_△EFK=$\frac{1}{2}$（t-6）•6=3（t-6），EH²=EF²=6²+（t-6）²，
∴S_△EMH=$\frac{{6}^{2}+（t-6）^{2}}{{6}^{2}}$•3（t-6），
∴S=S_{正方形EFGH}-S_△EHM=6²+（t-6）²-$\frac{{6}^{2}+（t-6）^{2}}{{6}^{2}}$•3（t-6）=-$\frac{1}{12}$t³+$\frac{5}{2}$t²-24t=108．

（3）存在．t=3+$\sqrt{33}$．
理由：如图6中，作EK⊥BC于K，

∵△EFK∽△EDH，
∴$\frac{EF}{ED}$=$\frac{EK}{EH}$，
∴EF•EH=EK•ED，
∴EF²=EK•ED，
∴6²+（t-6）²=6（16-t），
∴t=3+$\sqrt{33}$或3-$\sqrt{33}$（舍弃）．
∴t=（3+$\sqrt{33}$）秒时，点D落在正方形EFGH的GH边上．

点评 本题考查四边形综合题、全等三角形的判定和性质．相似三角形的判定和性质、勾股定理等知识，解题的关键是学会分类讨论，需要正确画出图形，学会利用分割法求面积，学会转化的思想解决问题，把问题转化为方程去思考，属于中考压轴题．