
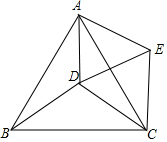
 若D是△ABC内一点,△ABC与△ADE任为等边三角形,若∠BDC=100°,∠ADB=α,则α为多少度时△CDE是等腰三角形.
若D是△ABC内一点,△ABC与△ADE任为等边三角形,若∠BDC=100°,∠ADB=α,则α为多少度时△CDE是等腰三角形. 分析 证明△ABD≌△ACE,得到BD=CE,结合BD=CD,即可解决问题.
解答 解:∵△ABC、△ADE均为等边三角形,
∴∠BAC=∠DAE=60°,AB=AC,AD=AE;
∴∠BAD=∠CAE;
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵△CDE为等腰三角形,
∴BD=CD,CD=CE,
∵∠BDC=100°,
∴∠DBC=40°,
∴∠ABD=20°,
∴∠BAD=40°,
∴∠ADB=120°,
则α为120度时△CDE是等腰三角形.
点评 此题考查等边三角形性质问题,该题以等边三角形为载体,以全等三角形的判定及其性质的应用为核心构造而成;对综合的分析问题解决问题的能力提出了一定的要求.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕EF交AD于E,交BC于F.请用直尺和圆规画出折痕EF,并求出△ABE的面积.(长方形的对边平行且相等,四个角都为直角)
已知:长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕EF交AD于E,交BC于F.请用直尺和圆规画出折痕EF,并求出△ABE的面积.(长方形的对边平行且相等,四个角都为直角)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(单位:克) | -4 | -3 | -1 | 0 | 2 | 4 |
| 袋 数 | 1 | 3 | 4 | 4 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com