
分析 8、4和6的最小公倍数是24,都化为分母为24的分数,然后把它们之间的分母是24的所有分数写出,再约分化成分母是8的最简分数,即可得解.
解答 解:$\frac{1}{4}=\frac{6}{24}$,$\frac{5}{6}=\frac{20}{24}$,
24÷8=3,在$\frac{6}{24}$和$\frac{20}{24}$之间,是分子3的倍数的有$\frac{9}{24}、\frac{12}{24}、\frac{15}{24}$、$\frac{18}{24}$,
所以分母为8,且比$\frac{1}{4}$大、比$\frac{5}{6}$小的最简分数,这个最简分数可以是$\frac{3}{8}、\frac{5}{8}$.
故答案为:$\frac{3}{8}$或$\frac{5}{8}$.
点评 本题考查了最简分数,灵活应用约分和通分的知识来求解最简分数是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x
如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
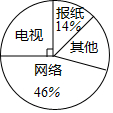 小明为了解他所居住小区居民最近“接受信息的最主要渠道”,利用课余时间,问卷调查了他所居住小区的居民,数据整理后,绘制成如下的扇形统计图.如果填写“接受信息的最主要渠道”是“网络”的人数有276名,试问:
小明为了解他所居住小区居民最近“接受信息的最主要渠道”,利用课余时间,问卷调查了他所居住小区的居民,数据整理后,绘制成如下的扇形统计图.如果填写“接受信息的最主要渠道”是“网络”的人数有276名,试问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 大于0.5 | B. | 1 | C. | 等于0.5 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com