练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图⊙O为△ABC的外接圆，∠A=70°，则∠BCO的度数为20°．

    分析 连结OB，如图，先根据圆周角定理得到∠BOC=2∠A=140°，然后根据等腰三角形的性质和三角形内角和定理计算∠BCO的度数．

    解答 解：连结OB，如图，∠BOC=2∠A=2×70°=140°，
    ∵OB=OC，
    ∴∠CBO=∠BCO，
    ∴∠BCO=$\frac{1}{2}$（180°-∠BOC）=$\frac{1}{2}$×（180°-140°）=20°．
    故答案为：20°．

    点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等腰三角形的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

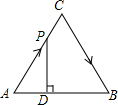    5．如图，△ABC是边长为4cm的等边三角形，动点P从点A出发，以2cm/s的速度沿A→C→B运动，到达B点即停止运动，过点P作PD⊥AB于点D，设运动时间为x（s），△ADP的面积为y（cm2），则能够反映y与x之间函数关系的图象大致是（　　）
    A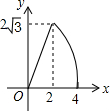．B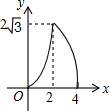．C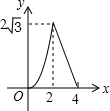．D．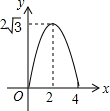

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

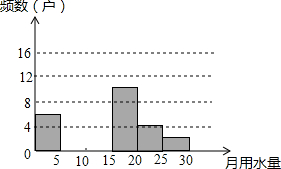    6．七（1）班同学为了解某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理：
    月均用水量x（t）频数（户）频率
    0＜x≤5612%
    5＜x≤101224%
    10＜x≤151632%
    15＜x≤201020%
    20＜x≤2548%
    25＜x≤3024%
    解答以下问题：
    （Ⅰ）把上面的频数分布表和频数分布直方图补充完整；
    （Ⅱ）观察上面的 频数分布表和频数分布直方图可知组距是5；
    （Ⅲ）本次随机调查了多少户家庭？
    （Ⅳ）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量不少于20t的家庭大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

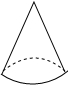    3．用一个平行于底面的平面去截如图放置的一个圆锥，将其分成上下两个几何体，如果设上面的小圆锥体积为x，下面的圆台体积为y，当截面由顶点向下平移时，y与x满足的函数关系的图象是（　　）
    A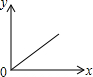．B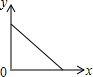．C．D．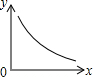

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，Rt△ABC在第一象限，∠BAC=90°，AB=AC=2，点A在直线y=x上，其中点A的横坐标为1，且AB∥x轴，AC∥y轴，若双曲线y=$\frac{k}{x}$（k≠0）与△ABC有交点，则k的取值范围是1≤k≤4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知一个多边形的内角和等于这个多边形外角和的2倍，则这个多边形的边数是（　　）
    A．4B．5C．6D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．-2的相反数等于（　　）
    A．$\frac{1}{2}$B．-$\frac{1}{2}$C．-2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．平行四边形ABCD对角线交于点O，下列式子一定成立的是（　　）
    A．AC⊥BDB．OA=OCC．AC=BDD．AO=OD

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．不等式组$\left\{\begin{array}{l}2-x≥0\\ 3x+2＞-1\end{array}\right.$的解集是-1＜x≤2．

    查看答案和解析>>

    同步练习册答案