
【题目】如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是 .

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
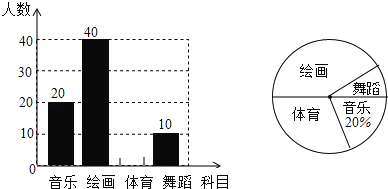
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a= 人,其中选择“绘画”的学生人数占抽样人数的百分比为b= ;
(2)补全条形统计图;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
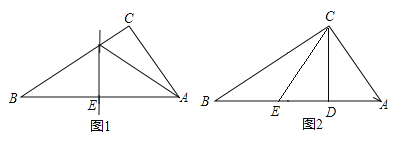
【题目】在数学实验课上,李静同学剪了两张直角三角形纸片,进行如下的操作:
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为 ;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k为常数,k≠1).
(k为常数,k≠1).
(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1、x2)、B(x2、y2),当y1>y2时,试比较x1与x2的大小;
(4)若在其图象上任取一点,向x轴和y轴作垂线,若所得矩形面积为6,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次 | 第二次 | 第三次 | |
A产品单价(元/件) | 6 | 5.2 | 6.5 |
B产品单价(元/件) | 3.5 | 4 | 3 |
并求得了A产品三次单价的平均数和方差:
![]() ;SA2=
;SA2=![]() [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=![]()
(1)补全“A、B产品单价变化的折线图”,B产品第三次的单价比上一次的单价降低了百分之多少?
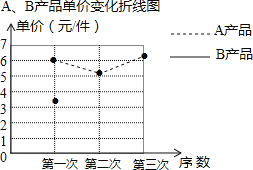
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件.
则A产品这四次单价的中位数是 元/件.
若A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,则B产品的第四次单价为 元/件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.
其中所有正确结论的序号是( )
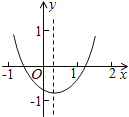
A.③④ B.②③ C.①④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=![]() 和y=
和y=![]() 的图象分别是l1和l2,设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2,设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )

A.8 B.9 C.10 D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4![]() ,则△BEF的面积是( )
,则△BEF的面积是( )
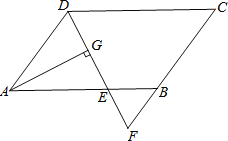
A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com