
【题目】百货商店服装专柜在销售中发现:某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.为占有市场份额,在确保盈利的前提下.
(1)降价多少元时,每星期盈利为6125元.
(2)降价多少元时,每星期盈利额最大,最大盈利额是多少?
【答案】
(1)解:设降价x元时,每星期盈利为6125元,
根据题意,得:(20﹣x)(300+20x)=6125,
解得:x=2.5,
答:降价2.5元时,每星期盈利为6125元
(2)解:设降价x元时,每星期的盈利为y元,
则y=(60﹣x)(300+20x)﹣40(300+20x)=﹣20x2+100x+6000.
因为降价要确保盈利,所以40<60﹣x≤60,
解得:0≤x<20,
∴当x= ![]() =2.5时,y有最大值
=2.5时,y有最大值 ![]() =6125,
=6125,
答:当降价2.5元时,利润最大且为6125元
【解析】(1)设降价x元时,每星期盈利为6125元,根据:每件利润×销售量=总利润,列方程求解可得;(2)根据:利润=单件利润×售出的总件数列出函数表达式,根据x=﹣ ![]() 时,y有最大值.
时,y有最大值.


科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣12+15﹣|﹣7﹣8|
(2)(﹣3)×(﹣9)﹣(﹣5)
(3)![]()
(4)![]()
化简:(5)![]()
(6)7a+3(a-3b)-2(b-3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
①四边形ABCD是菱形;
②四边形ABCD是中心对称图形;
③四边形ABCD是轴对称图形;
④AC=BD.
其中正确的是(写上正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2). 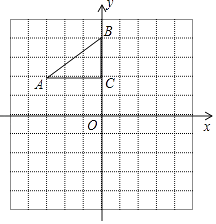
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在坐标系中作出旋转中心S并写出旋转中心S的坐标:S
(4)在x轴上有一点P,使得PA+PB的值最小,请作图标出P点并写出点P的坐标.P .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( ) 
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com