
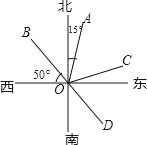
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
(1)若∠AOC=∠AOB,求OC的方向;
(2)OD是OB的反向延长线,求OD的方向;
(3)∠BOD可看作是OB绕点O顺时针方向旋转至OD,作∠BOD的平分线OE,求OE的方向.
【答案】(1)OC的方向是北偏东70°(2)OD的方向是南偏东40°(3)OE的方向是东偏北40°
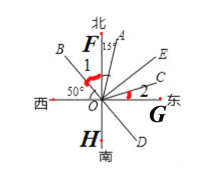
【解析】试题分析:(1)先根据OB的方向是西偏北50°求出∠1的度数,进而求出∠FOC的度数即可;(2)根据OB的方向是西偏北50°求出∠DOH的度数,即可求出OD的方向;(3)根据OE是∠BOD的平分线,可知∠DOE=90°,进而可求出∠GOE的度数可知OE的方向;
解:(1)∵OB的方向是西偏北50°,
∴∠1=90°﹣50°=40°,
∴∠AOB=40°+15°=55°,
∵∠AOC=∠AOB,
∴∠AOC=55°,
∴∠FOC=∠AOF+∠AOC=15°+55°=70°,
∴OC的方向是北偏东70°;
(2)∵OB的方向是西偏北50°,
∴∠1=40°,
∴∠DOH=40°,
∴OD的方向是南偏东40°;
(3)∵OE是∠BOD的平分线,
∴∠DOE=90°,
∵∠DOH=∠1=40°,
∴∠DOG=50°,
∴∠GOE=40°,
∴OE的方向是东偏北40°.


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程3x2=2x﹣1的二次项系数、一次项系数、常数项分别是( )
A.3,﹣2,﹣1B.3,2,﹣1C.﹣3,﹣2,1D.3,﹣2,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要得到函数y=x2的图象只要把函数y=(x﹣3)2的图象( )
A.向左平移3个单位B.向右平移3个单位
C.向上平移3个单位D.向下平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.

问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°.
(1)求点D到EF的距离.
(2)若AE=a,则S△DEF= (用含字母a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B、C、D在数轴上的位置如图1所示,已知AB=3,BC=2,CD=4.
(1)若点C为原点,则点A表示的数是 ;
(2)若点A、B、C、D分别表示有理数a,b,c,d,则|a﹣c|+|d﹣b|﹣|a﹣d|= ;
(3)如图2,点P、Q分别从A、D两点同时出发,点P沿线段AB以每秒1个单位长度的速度向右运动,到达B点后立即按原速折返;点Q沿线段CD以每秒2个单位长度的速度向左运动,到达C点后立即按原速折返.当P、Q中的某点回到出发点时,两点同时停止运动.
①当点停止运动时,求点P、Q之间的距离;
②设运动时间为t(单位:秒),则t为何值时,PQ=5?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2m x+m2+m+1的图像与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图像关于x轴翻折,所得图像的顶点为D,若CD=8.求四边形ACBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国爱眼日是每年的6月6日,2013年世界爱眼日主题确定为“关爱青少年眼健康”,某中学为了解该校学生的视力情况,采用抽样调查的方式,从视力正常、轻度近视、中度近视、重度近视四个方面调查了若干名学生的视力情况,并根据调查结果制作了如下两幅统计图. 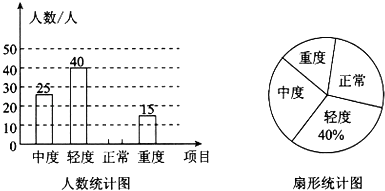
根据图中提供的信息解答下列问题:
(1)一共随机调查了多少人?
(2)补全人数统计图;
(3)若该校共有1500名学生,请你估计该校学生视力正常的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为极大地满足人民生活的需求,丰富市场供应,某区农村温棚设施农业迅速发展,温棚种植面积在不断扩大.在耕地上培成一行一行的长方形土埂,按顺序间隔种植不同农作物的方法叫分垄间隔套种.科学研究表明:在塑料温棚中分垄间隔套种高、矮不同的蔬菜和水果(同一种紧挨在一起种植不超过两垄),可增加它们的光合作用,提高单位面积的产量和经济效益.
现有一个种植总面积为540 m2的长方形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 30 | 160 | 1.1 |
草莓 | 15 | 50 | 1.6 |
(1)若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案,分别是哪几种;
垄,通过计算说明共有几种种植方案,分别是哪几种;
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com