
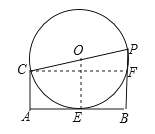
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 . 
【答案】![]()
【解析】解:当AB与⊙O相切时,PB的值最大,
如图,设AB与⊙O相切于E,连接OE,则OE⊥AB,
过点C作CF⊥PB于F,
∵CA⊥AB,DB⊥AB,
∴AC∥OE∥PB,
四边形ABPC是矩形,
∴CF=AB=6,
∵CO=OP,
∴AE=BE,
设PB=x,则PC=2OE=2+x,PF=x﹣2,
∴(x+2)2=(x﹣2)2+62 ,
解得;x=![]() ,
,
∴BP最大值为:![]() ,
,
所以答案是:![]() .
. 
【考点精析】根据题目的已知条件,利用直线与圆的三种位置关系的相关知识可以得到问题的答案,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )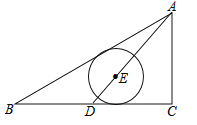
A.![]() ≤R≤
≤R≤![]()
B.![]() ≤R≤
≤R≤![]()
C.![]() ≤R≤2
≤R≤2
D.1≤R≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )

A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
查看答案和解析>>
科目:初中数学 来源: 题型:
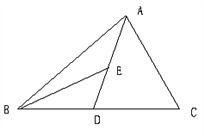
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作图:在△BED中作出BD边上的高EF;BE边上的高DG;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高EF为多少?若BE=6,求△BED中BE边上的高DG为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:![]() 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有![]() .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)![]() ;(2)
;(2)![]() ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com