
 已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)
已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)  心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
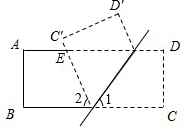 如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.
如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com