
【题目】如图,若![]() 内一点
内一点![]() 满足
满足![]() ,则点
,则点![]() 为
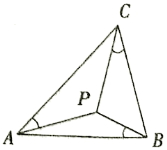
为![]() 的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形
的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形![]() 中,
中,![]() .若
.若![]() 为
为![]() 的布洛卡点,
的布洛卡点,![]() ,则
,则![]() 的值为( )
的值为( )
A.10B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
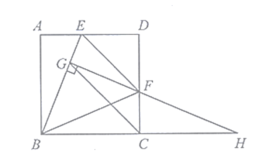
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为12,E是边CD的中点,连接AE,折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为![]() 的中点.
的中点.
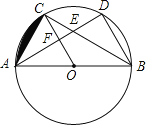
(1)求证:OF∥BD;
(2)若![]() ,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,动点
,动点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .设
.设![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .设四边形
.设四边形![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() (平方单位),
(平方单位),![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.

(1)求![]() 的长;
的长;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)求![]() 与
与![]() 的函数关系式,并直接写出自变量取值范围.
的函数关系式,并直接写出自变量取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
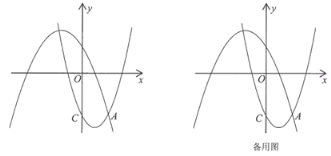
【题目】如图,在平面直角坐标系xOy中,抛物线L1:![]() 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2:![]() 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师从本校九年级质量检测的成绩中随机地抽取一些同学的数学成绩做质量分析,他先按照等级绘制这些人数学成绩的扇形统计图,如图(1)所示,数学成绩等级标准见表1,又按分数段绘制成绩分布表,如表2,
表1
等级 | 分数x的范围 |
A | a≤x≤100 |
B | 80≤x<a |
C | 60≤x<80 |
D | 0≤x<60 |
表2
分数段 | x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
人数 | 5 | 10 | m | 12 | n |
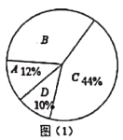
分数段为90≤x≤100的n个人中,其成绩的中位数是95分.
根据以上信息回答下面问题:
(1)王老师抽查了多少人?m、n的值分别是多少;
(2)小明在此考试中得了95分,他说自己在这些考试中数学成绩是A等级,他说的对吗?为什么?
(3)若此次测试数学学科普高的预测线是70分,该校九年级有900名学生,求数学学科达到普高预测线的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地摊上的一种玩具,已知其进价为![]() 元个,试销阶段发现将售价定为
元个,试销阶段发现将售价定为![]() 元/个时,每天可销售
元/个时,每天可销售![]() 个,后来为了扩大销售量,适当降低了售价,销售量
个,后来为了扩大销售量,适当降低了售价,销售量![]() (个)与降价
(个)与降价![]() (元)的关系如图所示.
(元)的关系如图所示.
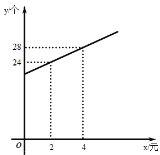
![]() 求销量
求销量![]() 与降价
与降价![]() 之间的关系式;
之间的关系式;
![]() 该玩具每个降价多少元,可以恰好获得
该玩具每个降价多少元,可以恰好获得![]() 元的利润?
元的利润?
![]() 若要使得平均每天销售这种玩具的利润
若要使得平均每天销售这种玩具的利润![]() 最大,则每个玩具应该降价多少元?最大的利润
最大,则每个玩具应该降价多少元?最大的利润![]() 为多少元?
为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
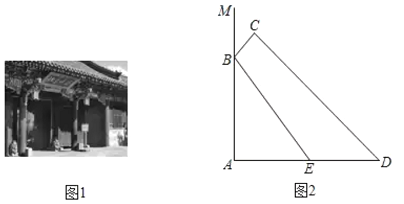
【题目】如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段![]() 就是悬挂在墙壁
就是悬挂在墙壁![]() 上的某块匾额的截面示意图.已知
上的某块匾额的截面示意图.已知![]() 米,
米,![]() .从水平地面点
.从水平地面点![]() 处看点
处看点![]() ,仰角
,仰角![]() ,从点
,从点![]() 处看点
处看点![]() ,仰角
,仰角![]() .且
.且![]() 米,求匾额悬挂的高度
米,求匾额悬挂的高度![]() 的长.(参考数据:
的长.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com