
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转60°,得到△AED,点B、C的对应点分别是E、D.F为AC的中点,连接BF、DF、BE,DF与EA相交于点G,BE与AC相交于点H.
(1)如图1,求证:四边形BFDE为平行四边形;
(2)如图2,连接CE,在不添加任何辅助线与字母的情况下,请直接写出所有与△AEC全等的三角形.

【答案】(1)见解析;(2)△ADE,△ABC,△ADF与△ACE全等,理由见解析
【解析】
(1)由直角三角形的性质可得BF=BC,由旋转的性质可得∠ACB=∠DAF=60°,CA=DA,AF=CB,由“SAS”可证△AFD≌△CBA,可得DF=AB=BE,且BF=DE,即可得四边形BFDE是平行四边形;
(2)由“SAS”可证△BAC≌△EAC,△ACE≌△ADE,可求解.
证明:(1)∵点F是边AC中点,∠ABC=90°,
∴BF=![]() AC,
AC,
又∵∠BAC=30°,
∴BC=![]() AC,∠ACB=60°,
AC,∠ACB=60°,
∴BF=BC,
∵将△ABC绕点A顺时针旋转60°,得到△AED,
∴∠BAE=∠DAC=60°,CA=DA,DE=BC,
∴DE=BF,△BCF和△BAE为等边三角形,
∴BE=AB=AE,
∴AF=BC,∠CAD=∠C=60°,AC=AD,
∴△AFD≌△CBA(SAS),
∴DF=AB,
∴DF=BE,且BF=DE,
∴四边形BFDE是平行四边形;
(2)△ADE,△ABC,△ADF与△ACE全等;
理由如下:由(1)可得:
∵∠BAE=60°,∠BAC=30°,
∴∠BAC=∠CAE=30°,且AC=AC,AB=AE,
∴△BAC≌△EAC(SAS),
∵∠CAE=∠DAE=30°,AC=AD,AE=AE,
∴△ACE≌△ADE(SAS),
∵△AFD≌△CBA(已证),
∴△EAC≌△FDA.
故:△ADE,△ABC,△ADF与△ACE全等


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
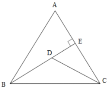
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.

(1)求证:△DAE≌△DCF;
(2)求证:△ABG∽△CFG;
(3)若正方形ABCD的的边长为2,G为BC的中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D是AB的中点,E是直线BC上一点,把△BDE沿直线ED翻折后,点B落在点F处,当FD⊥BC时,线段BE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=![]() +bx+c的图象交x轴于点A,B,交y轴于点C(0,﹣2),一次函数y=
+bx+c的图象交x轴于点A,B,交y轴于点C(0,﹣2),一次函数y=![]() x+n的图象经过A,C两点,点P为直线AC下方二次函数图象上的一个动点,直线BP交线段AC于点E,PF⊥AC于点F.
x+n的图象经过A,C两点,点P为直线AC下方二次函数图象上的一个动点,直线BP交线段AC于点E,PF⊥AC于点F.
(1)求二次函数的解析式;
(2)求![]() 的最大值及此时点P的坐标;
的最大值及此时点P的坐标;
(3)连接CP,是否存在点P,使得Rt△CPF中的一个锐角恰好等于2∠BAC?若存在,请直接写出点P的坐标;否则,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
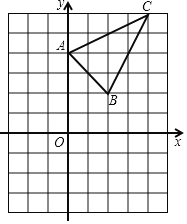
【题目】如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)(正方形网格中,每个小正方形的边长为1)
(1)画出△ABC向下平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2,直接写出点C2的坐标和△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
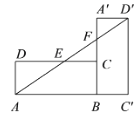
【题目】如图,矩形ABCD中,AD=1,AB=![]() .将矩形ABCD绕着点B顺时针旋转90°得到矩形
.将矩形ABCD绕着点B顺时针旋转90°得到矩形![]() .联结
.联结![]() ,分别交边CD,
,分别交边CD,![]() 于E、F.如果AE=
于E、F.如果AE=![]() ,那么
,那么![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
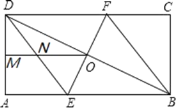
【题目】如图,在矩形ABCD中,过BD的中点O做EF⊥BD,分别与AB、CD交于点E、F.连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若M是AD中点,联结OM与DE交于点N,AD=OM=4,则ON的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
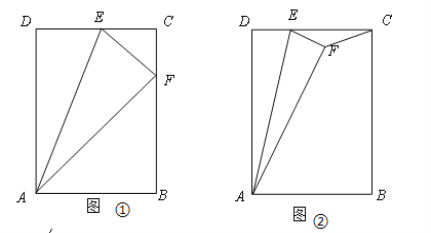
【题目】在矩形ABCD中,AB=3,AD=5,E是射线DC上的点,连接AE,将△ADE沿直线AE翻折得△AFE.
(1)如图①,点F恰好在BC上,求证:△ABF∽△FCE;
(2)如图②,点F在矩形ABCD内,连接CF,若DE=1,求△EFC的面积;
(3)若以点E、F、C为顶点的三角形是直角三角形,则DE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com