
 于点A,连接OA并延长,与双曲线
于点A,连接OA并延长,与双曲线 交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.
交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.
 时,求四边形APFH的面积.
时,求四边形APFH的面积. 交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积.
交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积. ,四边形BDFH的面积为______.(直接写出答案)
,四边形BDFH的面积为______.(直接写出答案) xy=
xy= ,
, =2;
=2; 交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,
交于点F,FH垂直于x轴,垂足为点H,连接BH、DF, ,
, ,四边形BDFH的面积为2|k|.
,四边形BDFH的面积为2|k|.

科目:初中数学 来源: 题型:
| 1 | x |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 于点A,连接OA并延长,与双曲线
于点A,连接OA并延长,与双曲线 交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.
交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.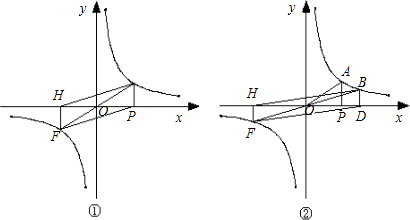
 时,求四边形APFH的面积.
时,求四边形APFH的面积. 交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积.
交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积. ,四边形BDFH的面积为______.(直接写出答案)
,四边形BDFH的面积为______.(直接写出答案)查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江丽水卷)数学(解析版) 题型:解答题
如图1,点A是x轴正半轴上的动点,点B的坐标为(0,4),M是线段AB的中点。将点M绕点A顺时针方向旋转900得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点。连结AC,BC,CD,设点A的横坐标为t,

(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段CD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到 ,再将A,B,
,再将A,B, 为顶点的四边形沿
为顶点的四边形沿 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形。请直接写出符合上述条件的点
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形。请直接写出符合上述条件的点 坐标,
坐标,
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广西南宁初中学校城乡共同体中考模拟数学试卷(解析版) 题型:选择题
如图,点A是y轴正半轴上的一个定点,点B是反比例函数y= (x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( )
(x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( )

(A) 逐渐增大 (B) 逐渐减小 (C) 不变 (D) 先增大后减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com