
【题目】如图,矩形ABCD的对角线交于点O,点E是矩形外一点,![]() ,
,![]() ,
,![]() ,连接AE交BD于点F、连接CF.
,连接AE交BD于点F、连接CF.
![]() 求证:四边形BECO是菱形;
求证:四边形BECO是菱形;
![]() 填空:若
填空:若![]() ,则线段CF的长为______.
,则线段CF的长为______.

科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
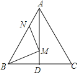
【题目】如图,在等边△ABC中,AB=9,N为AB上一点,且AN=3,BC的高线AD交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆E是三角形ABC的外接圆, ∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,必然事件是( )
A. 抛掷![]() 个均匀的骰子,出现
个均匀的骰子,出现![]() 点向上B. 两条直线被第三条直线所截,同位角相等
点向上B. 两条直线被第三条直线所截,同位角相等
C. ![]() 人中至少有
人中至少有![]() 人的生日相同D. 有理数的绝对值是非负数
人的生日相同D. 有理数的绝对值是非负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .
.

(1)如图中的图1,求证:![]() ;
;
(2)如图中的图2,![]() 是
是![]() 的中点,若
的中点,若![]() ,
,![]() ,在不添加任何辅助线的情况下,请找出图中的四个三角形,使得每个三角形的面积都等于
,在不添加任何辅助线的情况下,请找出图中的四个三角形,使得每个三角形的面积都等于![]() 面积的
面积的![]() 倍,并说明理由.
倍,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
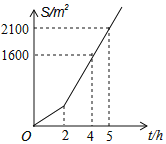
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
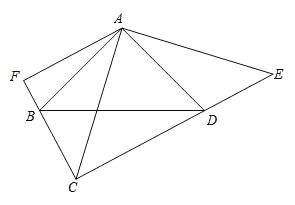
【题目】如图, BAD CAE 90 , AB AD , AE AC , ABD ADB ACE AEC 45 ,AF CF ,垂足为 F .
(1)若 AC 10 ,求四边形 ABCD 的面积;
(2)求证: CE 2 AF .
查看答案和解析>>
科目:初中数学 来源: 题型:
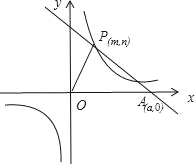
【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y=![]() (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+![]() .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠![]() ,求OP2的最小值.
,求OP2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com