
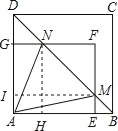
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

【答案】(1)证明见解析;(2)![]() c(a+b﹣c);(3)证明见解析.
c(a+b﹣c);(3)证明见解析.
【解析】试题分析:(1)首先过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,可得△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,则可求得BN=![]() b,DM=
b,DM=![]() a,继而求得答案;
a,继而求得答案;
(2)由S△AMN=S△ABD-S△ABM-S△ADN,可得S△AMN=![]() c2-
c2-![]() c(c-a)-
c(c-a)-![]() c(c-b),继而求得答案;
c(c-b),继而求得答案;
(3)易证得∴∠DMA=∠BAN,又由∠ABD=∠ADB=45°,可证得△ADM∽△NBA,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,
∴BN=![]() NH=
NH=![]() AG=
AG=![]() b,DM=
b,DM=![]() MI=
MI=![]() AE=
AE=![]() a,
a,
∴![]() ;
;
(2)S△AMN=S△ABD﹣S△ABM﹣S△ADN
=![]() ABAD﹣
ABAD﹣![]() ABME﹣
ABME﹣![]() ADNG
ADNG
=![]() c2﹣
c2﹣![]() c(c﹣a)﹣
c(c﹣a)﹣![]() c(c﹣b)
c(c﹣b)
=![]() c(c﹣c+a﹣c+b)
c(c﹣c+a﹣c+b)
=![]() c(a+b﹣c);
c(a+b﹣c);
(3)∵∠DMA=∠ABD+∠MAB=∠MAB+45°,∠BAN=∠MAB+∠MAN=∠MAB+45°,
∴∠DMA=∠BAN,
∵∠ABD=∠ADB=45°,
∴△ADM∽△NBA,
∴![]() ,
,
∵DM=![]() a,BN=
a,BN=![]() b,
b,
∴c2=2ab.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
(1)求证:E是AD中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB的高为16m,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为 60°,在楼顶B处测得塔顶D处的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高.(![]() =1.73,结果保留一位小数.)
=1.73,结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD是△ABC的角平分线,点E.F分别在边AB.BC上,且ED∥BC,EF∥AC,求证:
(1)BE等于CF
(2)∠ABC=60゜,∠ADB=100゜,求∠AEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题
(1)抽取了______名学生成绩;(2)请把条形统计图补充完整;
(3)扇形统计图中等级D所在的扇形的圆心角度数是______;
(4)若A,B,C代表合格,该校初二年级有300名学生,求全年级生物合格的学生共约多少人

查看答案和解析>>
科目:初中数学 来源: 题型:
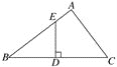
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
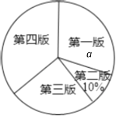
各版面选择人数的扇形统计图
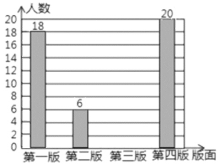
各版面选择人数的条形统计图
请根据图中信息,解答下列问题:
(1)a=______%,“第四版”对应扇形的圆心角为 °;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com