
����Ŀ����7�֣�ijѧУ�����ݽ�������ѡ����10��ͬѧ������ί���������ⶨ������4��������ѡ������ķ�����ȷ��ÿ���ݽ��ߵ����÷֣�����Ϊ10�֣���
����1��������ί�����ֵ�ƽ������
����2����������ί�������У�ȥ��һ����߷ֺ�һ����ͷ֣�Ȼ���ټ���������ֵ�lƽ������
����3��������ί�����ֵ���λЧ��
����4��������ί�����ֵ�������
Ϊ��̽�����������ĺ����ԣ��ȶ�ij��ͬѧ���ݽ��ɼ�������ͳ��ʵ�飮���������ͬѧ�ĵ÷�ͳ��ͼ��

��1���ֱ�����4�������������ͬѧ�ݽ������÷֣�
��2�����ݣ�1���еĽ��������ͳ�Ƶ�֪ʶ˵����Щ��������̨��Ϊ���ͬѧ�ݽ������÷֣���������ͬѧ�����÷֣�
���𰸡���1������1��7.7�֣�����2��8�֣�����3����λ��8������4��8��8.4����2������1�ͷ���4��8�֣�
��������
�������������ؼ�������ÿ�ַ����ļ��㷽������1������1��ƽ����=�ܷ�����10��
����2��ƽ����=ȥ��һ����߷ֺ�һ����ͷֵ��ܷ�����8��
����3��10�����ݣ���λ��Ӧ�ǵ�5���͵�6�����ݵ�ƽ������
����4�������ί�����У����ִ������ķ�����
��2�����Dz��ܼ�ֵ��Ӱ�죬�����������÷ֵ�ԭ������ų���
�����������1������1���÷֣�![]() ����3.2+7.0+7.8+3��8+3��8.4+9.8��=7.7��
����3.2+7.0+7.8+3��8+3��8.4+9.8��=7.7��
����2���÷֣�![]() ��7.0+7.8+3��8+3��8.4��=8��
��7.0+7.8+3��8+3��8.4��=8��
����3���÷֣�8��
����4���÷֣�8��8.4��
��2����Ϊ����1�е�ƽ�����ܼ�����ֵ��Ӱ�죬���ʺ���Ϊ���ͬѧ�ݽ������÷֣�
���Է���1���ʺ���Ϊ���÷ֵķ�����
��Ϊ����4�е�����������������ʧȥ��ʵ�����壬���Է���4���ʺ���Ϊ���÷ֵķ��������Ը�ͬѧ���÷�Ϊ8����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ABC���CDE�ǵ���ֱ�������Σ�ֱ�DZ�AC��CD��ͬһ��ֱ���ϣ���M��N�ֱ���б��AB��DE���е㣬��PΪAD���е㣬����AE��BD��
��1������PM��PN��������ϵ��λ�ù�ϵ����ֱ��д�����ۣ�
��2���ֽ�ͼ���еġ�CDE���ŵ�C˳ʱ����ת����0�㣼����90�㣩���õ�ͼ�ڣ�AE��MP��BD�ֱ��ڵ�G��H�����жϣ�1���еĽ����Ƿ����������������֤����������������˵�����ɣ�
��3����ͼ���еĵ���ֱ�������α��ֱ�������Σ�ʹBC=kAC��CD=kCE����ͼ�ۣ�д��PM��PN��������ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
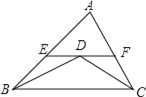
����Ŀ����ͼ����ABC�У�BDƽ�֡�ABC��CDƽ�֡�ACB������D��EF��BC����AB��AC�ֱ��ཻ��E��F������֪AB=9��AC=7������AEF���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͨ˿��֮·���ô��ĸ����ߩ�������ר����ȫ����ͨ����Σ�������ר��ͨ���Լӿ�������������һ��һ·�����߹��Һ͵����ľ�ó���������Ľ�������ʮ����Ҫ�����壮�������ڼ䣬һ�ж�������������������һ����ͨ�г���������������������ͬʱ����������ͨ�г���ʻ��ʱ��Ϊx��Сʱ��������֮��ľ���Ϊy��ǧ�ף���ͼ�е����߱�ʾy��x֮��ĺ�����ϵ������ͼ�����һ��̽����
����Ϣ��ȡ��
��1������������������� ǧ�ף����������� Сʱ������
��2����ͨ�г������յ㹲�� Сʱ����ͨ�г����ٶ��� ǧ��/Сʱ��
��������⡿
��3�������ٶȣ�
��4����ͨ�г���ʻtСʱ���������յ����������ʱ��ͨ�г�������ʻ����ǧ����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������и���:
(1)����:-22+|5-8|+24��(-3)��![]() ;
;
(2)���������:
������:3x2-[7x-(4x-3)-2x2];
���Ȼ���,����ֵ:![]() x-2
x-2![]() +
+![]() ,����x=-2,y=
,����x=-2,y=![]() ;
;
(3)�ⷽ��:
��32x-64=16x+32;
��-![]() =2-
=2-![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ��ѧ��ÿ����Ԫ�IJ���ɼ����£���λ���֣���
�ף�98��100��100��90��96��91��89��99��100��100��93
�ң�98��99��96��94��95��92��92��98��96��99��97
(1)�����ǵ�ƽ���ɼ��ֱ��Ƕ��٣�
(2)���ס��ҵ�11�ε�Ԫ����ɼ��ı���ֱ��Ƕ��٣�
(3)������λͬѧ�ijɼ�����ʲô�ص㣿
(4)����Ҫ����ѡ��һ�˲μӡ�ϣ��������������������ɼ�������ƽʱ�ɼ��ﵽ98�����ϲſ��ܽ������������ΪӦѡ˭�μ��������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ղ��������֤����
��֪����P��ֱ��CD�ϣ���BAP+��APD=180�㣬��1=��2��
��֤��AB��CD����E=��F��
֤�����ߡ�BAP+��APD=180��������֪��
��AB���� �������� ����
���BAP=�� �������� ����
���ߡ�1=��2������֪��
��3=�� ������1��
��4=�� ������2��
���3=�� ������ʽ�����ʣ�
��AE��PF������ ����
���E=��F������ ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���D��F�ֱ����߶�BC��AB�ϣ���EFB=60����DC=EF��
��1����֤���ı���EFCD��ƽ���ı��Σ�
��2����BF=EF����֤��AE=AD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���ABCD�����Σ�E��BD�ӳ�����һ�㣬F��DB�ӳ�����һ�㣬��DE=BF��������FΪһ���˵㣬��ͼ���ѱ�����ĸ��ijһ������һ���µ��߶Σ����벢֤������ͼ�����е�ijһ���߶���ȣ�ֻ��֤��һ���߶���ȼ��ɣ���

��1������ ��
��2�����룺 = ��
��3��֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com