
【题目】如图,四边形![]() 是
是![]() 的内接四边形.
的内接四边形.![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() .
.
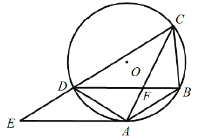
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)6
【解析】
(1)连接OA,由垂径定理易得OA⊥BD,再由AE∥BD,可得OA⊥AE,即可得证;
(2)由平行弦所夹的弧相等可推出BC=AD=AB=4,所以四边形ABCD为等腰梯形,过A作AP⊥CD于点P,过B作BQ⊥CD于点Q,易得PQ=AB=4,PD=CQ=0.5,然后利用勾股定理可求出BD,再证明四边形ABDE为平行四边形,可得AE=BD.
(1)如图,连接OA,
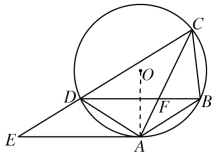
∵点A是![]() 的中点,
的中点,
∴OA⊥BD
又∵AE∥BD
∴OA⊥AE
∴AE为![]() 的切线.
的切线.
(2)∵AB∥CD
∴![]()
∴BC=AD=AB=4
∴四边形ABCD为等腰梯形
如图所示,过A作AP⊥CD于点P,过B作BQ⊥CD于点Q,
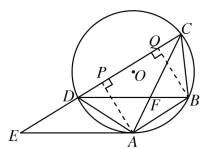
则四边形ABQP为矩形
∴PQ=AB=4
∵四边形ABCD为等腰梯形
∴AD=BQ,AP=BQ
∴Rt△ADP≌Rt△BCQ(HL)
∴PD=BQ=![]()
在Rt△BCQ中,CQ2+BQ2=BC2
在Rt△BDQ中,
BD2=DQ2+BQ2=![]()
∴BD=6
∵AE∥BD,AB∥DE
∴四边形ABDE为平行四边形
∴AE=BD=6


科目:初中数学 来源: 题型:
【题目】某水果批发市场规定,批发苹果不少于![]() 时,批发价为5元/
时,批发价为5元/![]() .小王携带现金4000元到这市场采购苹果,并以批发价买进.
.小王携带现金4000元到这市场采购苹果,并以批发价买进.
(Ⅰ)根据题意,填表:
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
(Ⅱ)设购买的苹果为![]() ,小王付款后还剩余现金
,小王付款后还剩余现金![]() 元.求
元.求![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)根据题意填空:若小王剩余现金为700元,则他购买__________![]() 的苹果.
的苹果.
查看答案和解析>>
科目:初中数学 来源: 题型:
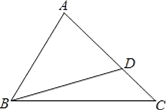
【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
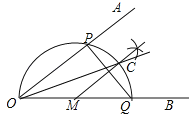
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 ![]() 于点C;
于点C;
步骤3:画射线OC.
则下列判断:①![]() =
=![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(用虚线表示画图过程,实线表示画图结果)
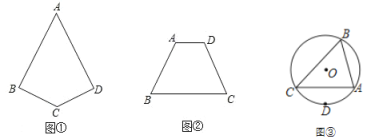
(1)如图①,四边形 ABCD 中,AB=AD,∠B=∠D,画出四边形 ABCD 的对称轴 m;
(2)如图②,四边形 ABCD 中,AD∥BC,∠A=∠D,画出 BC 边的垂直平分线 n.
(3)如图③,△ABC 的外接圆的圆心是点 O,D 是![]() 的中点,画一条直线把△ABC 分成面积相等的两部分.
的中点,画一条直线把△ABC 分成面积相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
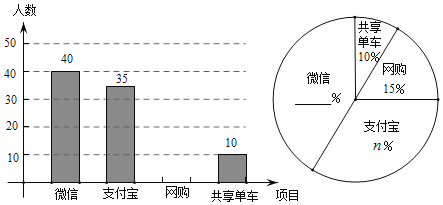
【题目】目前“微信”、“支付宝”、“共享单车“和“网购”给我们的生活带来了很多便利,九年级数学兴趣小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种),并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”,D同学最认可“网购”,从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com