
如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG.
(1)CH= .
(2)求DG的长.
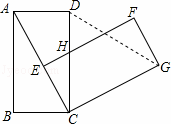
解:(1)在矩形ABCD中,∵AB=4,BC=3,
∴AC= =
=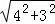 =5,
=5,
∵矩形ABCD绕点C按顺时针方向旋转得矩形CEFG,
∴CE=BC=3,
∵∠BAC+∠ACB=90°,∠ECH+∠ACB=90°,
∴∠BAC=∠ECH,
又∵∠B=∠CEH=90°,
∴△ABC∽△CEH,
∴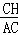 =
= ,
,
即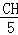 =
= ,
,
解得CH= ;
;
故答案为: ;
;
(2)如图,过点G作GM⊥CD于M,
∵∠ACB+∠ACD=∠GCM+∠ACD=90°,
∴∠ACB=∠GCM,
又∵∠B=∠GMC=90°,
∴△ABC∽△GMC,
∴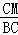 =
=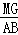 =
= ,
,
即 =
=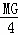 =
= ,
,
解得CM= ,MG=
,MG= ,
,
∴DM=CD﹣CM=4﹣ =
= ,
,
在Rt△DMG中,DG=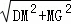 =
= =
= .
.



科目:初中数学 来源: 题型:
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)

查看答案和解析>>
科目:初中数学 来源: 题型:
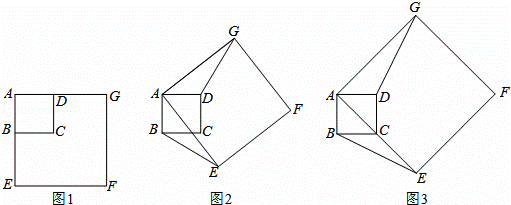
如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD的度数;
(3)如图3,如果α=45°,AB=2,AE=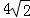 ,求点G到BE的距离.
,求点G到BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于 CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )

A. SAS B.ASA C.AAS D. SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于 点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC.

A. 1 B.2 C.3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
下列四个命题中,真命题是( )
A. 对角线互相垂直平分的四边形是正方形
B. 对角线垂直相等的四边形是菱形
C. 对角线相等且互相平分的四边形是矩形
D. 四边都相等的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com