
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����Ϊ��6��0������B��y����������ϣ���S��AOB=24��
��1�����B���ꣻ
��2������P��B������y�Ḻ�����˶����ٶ�ÿ��2����λ���˶�ʱ��t�룬��AOP�����ΪS����S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
��3���ڣ�2���������£���S��AOP��S��ABP=1��3����S��AOP+S��ABP=S��AOB �� ���߶�AB�Ĵ�ֱƽ�������Ƿ���ڵ�Q��ʹ�á�AOQ��������BPQ�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1���ߵ�A����Ϊ��6��0����
��OA=6��
��S��AOB=![]() ��OA��OB=24��
��OA��OB=24��
��OB=8��
���B������0��8����
��2����0��t��4ʱ��S=![]() ����8��2t����6=24��6t��
����8��2t����6=24��6t��
��t��4ʱ��S=![]() ����2t��8����6=6t��24��
����2t��8����6=6t��24��
��3����S��AOP+S��ABP=S��AOB ��
���P���߶�OB�ϣ�
��S��AOP��S��ABP=1��3��
��OP��BP=1��3��
�֡�OB=8��
��OP=2��BP=6��
�߶�AB�Ĵ�ֱƽ�����Ͻ�OB��E����AB��F��
��OB=8��OA=6��
��AB=![]() =10��
=10��
���F��������3��4����
��EF��AB����AOB=90�㣬
���BEF�ס�BAO��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�BE=![]() ��
��
��OE=8��![]() =
=![]() ��
��
���E��������0��![]() ����
����
��ֱ��EF�Ľ���ʽΪy=kx+b��
��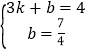 ��
��
��ã�k=![]() ��b=
��b=![]() ��
��
��ֱ��EF�Ľ���ʽΪy=![]() x+
x+![]() ��
��
�ߡ�AOQ��������BPQ�������ȣ���OA=BP��
��x=y����x=��y��
��x=yʱ��x=![]() x+
x+![]() ����ã�x=7��
����ã�x=7��
��Q��������7��7����
��x=��yʱ����x=![]() x+
x+![]() ����ã�x=��1��
����ã�x=��1��
��Q����������1��1����
��Q��������7��7����1��1����
����������1�����������ε������ʽ���OB�ij����ɣ�
��2����0��t��4��t��4������������������������ʽ���㼴�ɣ�
��3����������������ε������ʽ���OP��BP�ij����������������ε����������E�����꣬�����е������ȷ����F�����꣬���ô���ϵ�������ֱ��ef�Ľ���ʽ�����ݵȵ����������������ȣ����ǵĸ�Ҳ��ȷ�x=y��x=��y����������㼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD
��1����֤��CDΪ��O������
��2����DC+DA=6����O��ֱ��Ϊ10����AB�ij��ȡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����[a]��ʾ������a��������������磺[2.3]=2��[��4 ![]() ]=��5��[5]=5��
]=��5��[5]=5��
��1����[2 ![]() ]+[��3.6]��[��7]��ֵ��
]+[��3.6]��[��7]��ֵ��
��2����[a]=a��[a]����{2 ![]() }��[��2.4]+{��6
}��[��2.4]+{��6 ![]() }��
}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
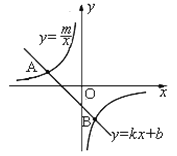
����Ŀ������ͼ����֪A��-4��2����B��n��-4����һ�κ���y=kx+b��ͼ��ͷ���������![]() ��ͼ����������㣮
��ͼ����������㣮
��1����m��n��ֵ��
��2����һ�κ����Ĺ�ϵʽ����
��3�����ͼ��ֱ��д��һ�κ���С�ڷ�����������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���5x2-4x-1=0�Ķ�����ϵ����һ����ϵ���ֱ�Ϊ�� ��
A. 5��4B. 5��-4C. 5,-1D. 5x2,4x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������A��B����A��ʾ��3����B���A���5.5����λ���ȣ����B��ʾ����Ϊ�� ��
A.��2.5��8.5
B.2.5��8.5
C.��2.5
D.��8.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
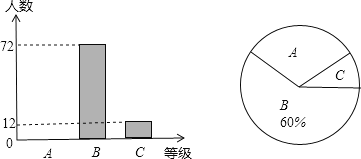
����Ŀ������ij��ѧΪ�˽�ѧ�������ʽ���״���������ȡ������ѧ�����в��ԣ����Խ����ΪA�����á�B���ϸ�C�����ϸ������ȼ��������ݲ��Խ�����Ƴ����������в�������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
��1���˴ε��鹲��ȡ�������ˣ�����ͳ��ͼ��C����Բ�ĽǵĶ���Ϊ������
��2����ȫ����ͳ��ͼ��
��3������У����1800��ѧ������������ʽ���״��Ϊ���ϸ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳����
��ͼ1��AB//CD����PAB=130�㣬��PCD=120�㣬���APC�Ķ�����
С����˼·�ǣ���P��PE//AB��ͨ��ƽ�������������APC��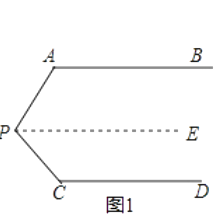
��1����С����˼·�����APC�Ķ�����
��2��������Ǩ�ơ���
��ͼ2��AB//CD����P������OM���˶����ǡ�PAB=������PCD=�£�����P��B��D����֮���˶�ʱ���ʡ�APC�������֮���к�������ϵ����˵�����ɣ�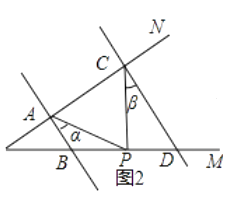
��3��������Ӧ�á���
�ڣ�2���������£������P��B��D��������˶�ʱ����P���O��B��D���㲻�غϣ�����ֱ��д����APC�������֮���������ϵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com