
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

【答案】(1)见解析 (2)见解析 (3)![]() m°
m°
【解析】分析:(1)如图1中,欲证明BD=EC,只要证明△DAB≌△EAC即可;
(2)如图2中,延长DC到E,使得DB=DE.首先证明△BDE是等边三角形,再证明△ABD≌△CBE即可解决问题;
(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.想办法证明△AFE≌△AFG,可得∠EAF=∠FAG=![]() m°.
m°.
详(1)证明:如图1中,
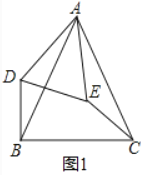
∵∠BAC=∠DAE,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
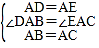 ,
,
∴△DAB≌△EAC,
∴BD=EC.
(2)证明:如图2中,延长DC到E,使得DB=DE.
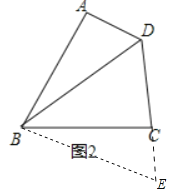
∵DB=DE,∠BDC=60°,
∴△BDE是等边三角形,
∴∠BD=BE,∠DBE=∠ABC=60°,
∴∠ABD=∠CBE,
∵AB=BC,
∴△ABD≌△CBE,
∴AD=EC,
∴BD=DE=DC+CE=DC+AD.
∴AD+CD=BD.
(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.

由(1)可知△EAB≌△GAC,
∴∠1=∠2,BE=CG,
∵BD=DC,∠BDE=∠CDM,DE=DM,
∴△EDB≌△MDC,
∴EM=CM=CG,∠EBC=∠MCD,
∵∠EBC=∠ACF,
∴∠MCD=∠ACF,
∴∠FCM=∠ACB=∠ABC,
∴∠1=3=∠2,
∴∠FCG=∠ACB=∠MCF,
∵CF=CF,CG=CM,
∴△CFG≌△CFM,
∴FG=FM,
∵ED=DM,DF⊥EM,
∴FE=FM=FG,
∵AE=AG,AF=AF,
∴△AFE≌△AFG,
∴∠EAF=∠FAG=![]() m°.
m°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(引例)
如图1,点A、B、D在同一条直线上,在直线同侧作两个等腰直角三角形△ABC和△BDE,BA=BC,BE=BD,连接AE、CD.则AE与CD的关系是 .

(模型建立)
如图2,在△ABC和△BDE中,BA=BC,BE=BD,∠ABC=∠DBE=α,连接AE、CD相交于点H.求证:①AE=CD;②∠AHC=α.
(拓展应用)
如图3,在四边形ABCD中,对角线AC与BD交于点O,∠BDC=90°,BD=CD,∠BAD=45°.若AB=3,AD=4,求AC2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
收集数据
(1)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是 .
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
整理数据
(2)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 °、 °;
②估计九年级A、B类学生一共有 名.
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
分析数据
(3)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 和一次函数y=k2x+b的图象交于点M(3,﹣
和一次函数y=k2x+b的图象交于点M(3,﹣![]() )和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
)和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在直角坐标系内的位置如图所示.
(1)请直接写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)计算△A1B1C1面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____,(请直接填写序号)
①2<2![]() <3;②四边形的内角和与外角和相等;③
<3;②四边形的内角和与外角和相等;③![]() 的立方根为4;
的立方根为4;
④一元二次方程x2﹣6x=10无实数根;
⑤若一组数据7,4,x,3,5,6的众数和中位数都是5,则这组数据的平均数也是5.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com