
 如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )
如图,平面直角坐标系中,分别以点A (-2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于( )| A. | $\sqrt{74}$ | B. | $\sqrt{74}$+3 | C. | $\sqrt{74}$-3 | D. | 3 |
分析 作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,根据两点之间线段最短得到此时PM+PN最小,再利用对称确定A′的坐标,接着利用两点间的距离公式计算出A′B的长,然后用A′B的长减去两个圆的半径即可得到MN的长,即得到PM+PN的最小值.
解答 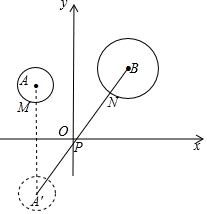 解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
则此时PM+PN最小,
∵点A坐标(-2,3),
∴点A′坐标(-2,-3),
∵点B(3,4),
∴A′B=$\sqrt{(3+2)^{2}+(4+3)^{2}}$=$\sqrt{74}$,
∴MN=A′B-BN-A′M=$\sqrt{74}$-2-1=$\sqrt{74}$-3,
∴PM+PN的最小值为$\sqrt{74}$-3.
故选C.
点评 本题考查了圆的综合题:掌握与圆有关的性质和关于x轴对称的点的坐标特征;会利用两点之间线段最短解决线段和的最小值问题;会运用两点间的距离公式计算线段的长;理解坐标与图形性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
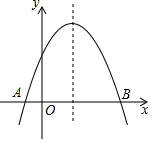 函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )
函数y=-x2+2(m-1)x+m+1的图象如图,它与x轴交于A,B两点,线段OA与OB的比为1:3,则m的值为( )| A. | $\frac{1}{3}$或2 | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
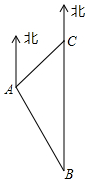 如图,某渔船航行至B处时,侧得一海岛位于B处的正北方向20(1+$\sqrt{3}$)海里的C处,为了防止意外,渔船请求A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位子B的北偏西300的方向上,求A,C之间的距离.
如图,某渔船航行至B处时,侧得一海岛位于B处的正北方向20(1+$\sqrt{3}$)海里的C处,为了防止意外,渔船请求A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位子B的北偏西300的方向上,求A,C之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com