
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,在边
的中点,在边![]() 上取点
上取点![]() ,使
,使![]() .绕点
.绕点![]() 旋转
旋转![]() ,得到
,得到![]() (点
(点![]() 、
、![]() 分别与点
分别与点![]() 、
、![]() 对应),当
对应),当![]() 时,则
时,则![]() ___________.
___________.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明在10次抛图钉的试验中发现3次钉朝上,由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子,出现6的概率是![]() 的意思是每6次就有1次掷得6
的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖
D. 在一次课堂进行的抛掷硬币试验中,某同学估计硬币落地后,正面朝上的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣![]() x+2与x轴交于点B,与y轴交于点C,二次函数y=﹣
x+2与x轴交于点B,与y轴交于点C,二次函数y=﹣![]() +bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的表达式;
(2)如图1,点D是抛物线第四象限上的一动点,连接DC,DB,当S△DCB=S△ABC时,求点D坐标;
(3)如图2,在(2)的条件下,点Q在CA的延长线上,连接DQ,AD,过点Q作QP∥y轴,交抛物线于P,若∠AQD=∠ACO+∠ADC,请求出PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点).
(1)在第一象限内找一点P,以格点P、A、B为顶点的三角形与△ABC相似但不全等,请写出符合条件格点P的坐标;
(2)请用直尺与圆规在第一象限内找到两个点M、N,使∠AMB=∠ANB=∠ACB.请保留作图痕迹,不要求写画法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上,将
上,将![]() 沿射线
沿射线![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,得到
重合,得到![]() (点
(点![]() 、
、![]() 分别与点
分别与点![]() 、
、![]() 对应),线段
对应),线段![]() 与
与![]() 轴交于点
轴交于点![]() ,线段
,线段![]() ,
,![]() 分别与直线
分别与直线![]() 交于点
交于点![]() ,
,![]() .
.
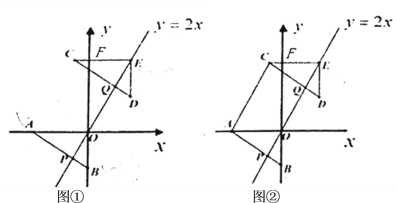
(1)求点![]() 的坐标;
的坐标;
(2)如图②,连接![]() ,四边形
,四边形![]() 的面积为__________(直接填空);
的面积为__________(直接填空);
(3)过点![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,当
,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
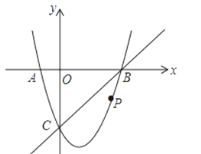
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.
(1)求这个二次函数y=x2+bx+c的解析式.
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.
(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com