
分析 (1)先根据A、B点对应的数找出线段AB的长度,再用AB的长度减去甲乙的速度和即可得出结论;
(2)设第n次爬行结束后,二者之间的距离为an(n为自然数).根据题意,罗列出部分an的值,根据数值的变化找出变化规律“a2n+1=|28.8-3.2n|,a2n+2=|35.2+3.2n|”,结合该规律即可解决问题.
解答 解:(1)∵数轴上两个定点A、B对应的数分别是-18和14,
∴线段AB的长度:AB=14-(-18)=32,
第1次爬行结束后,两只电子蚂蚁间的距离为:32-(1.5+1.7)=28.8.
故答案为:28.8.
(2)设第n次爬行结束后,二者之间的距离为an(n为自然数),
观察,发现规律:a1=32-3.2=28.8,a2=32+3.2=35.2,a3=32-3.2×2=25.6,a4=32+3.2×2=38.4,…,
∴a2n+1=|32-3.2(n+1)|=|28.8-3.2n|,a2n+2=|32+3.2(n+1)|=|35.2+3.2n|,
令a2n+1=0,即28.8-3.2n=0,解得:n=9,
此时,2n+1=2×9+1=19;
令a2n+2=0,即35.2+3.2n=0,解得:n=-11(舍去).
故答案为:19.
点评 本题考查了规律型中的图形的变化类、数轴上的点以及解一元一次方程,解题的关键是:(1)明白什么是相向运动;(2)找出变化规律“a2n+1=|28.8-3.2n|,a2n+2=|35.2+3.2n|”.本题属于中档题,难道不大,解决该题型题目时,依据题意,罗列出部分数据,根据数据的变化找出变化规律是关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 向左平移3个单位长度得到 | B. | 向右平移三个单位长度得到 | ||
| C. | 向上平移3个单位长度得到 | D. | 向下平移3个单位长度得到 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
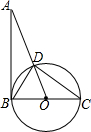 如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.
如图,AB=12,且AB为⊙O的切线,BC为⊙O的直径,AO与⊙O交于点D、AD=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是一个无理数 | |
| B. | 它是数轴上离原点$\sqrt{7}$个单位长度的点表示的数 | |
| C. | 若a<$\sqrt{7}$<a+1,则整数a为2 | |
| D. | 它表示面积为7的正方形的边长 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{2}+\sqrt{5}$)$\sqrt{7}$=$\sqrt{7}$×$\sqrt{7}$=7 | B. | ($\sqrt{5}+\sqrt{3}$)($\sqrt{5}-\sqrt{2}$)=5-$\sqrt{6}$ | C. | ($\sqrt{3}-\sqrt{2}$)($\sqrt{3}+\sqrt{2}$)=3-2=1 | D. | ($\sqrt{5}-\sqrt{3}$)2=5-3=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com