
 ,AC=3,则sinB为( )
,AC=3,则sinB为( )




 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源:山东省日照市2012年中考数学试题 题型:044
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知
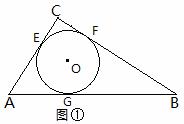
如图①⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..

(1)求证内切圆的半径r1=1;
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
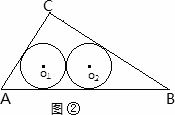
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.
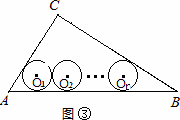
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东日照卷)数学(带解析) 题型:解答题
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知:
如图①⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1="1;"
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.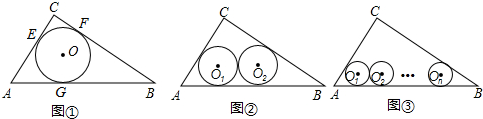
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东日照卷)数学(解析版) 题型:解答题
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知:
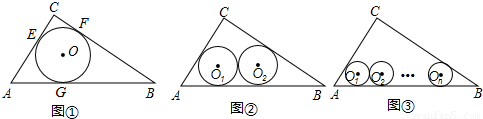
如图① ⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1=1;
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知
如图① ⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1=1;
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com